Understanding How Power Factor is Calculated
Power Quality Analysis Training
Our customized live online or in‑person group training can be delivered to your staff at your location.
- Live Online
- 12 hours Instructor-led
- Group Training Available
Download Our OSHA 3875 Fact Sheet – Electrical PPE for Power Industry Workers
- Follow rules for rubber gloves, arc-rated PPE, and inspection procedures
- Learn employer obligations for testing, certification, and training
- Protect workers from arc flash and electrical shock injuries
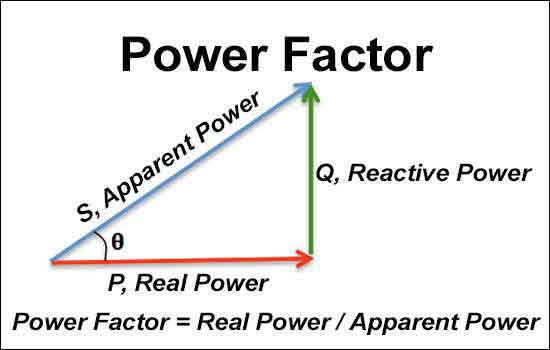
How Power Factor is Calculated? By PF = kW/kVA = cos φ, using real power, apparent power, and phase angle in AC circuits to assess efficiency, reactive power, voltage, current, and load balance.
How Power Factor Is Calculated?
Power factor equals kW/kVA = cos φ, from the phase angle between voltage and current in AC circuits.
✅ Formula: PF = kW/kVA; ratio of real to apparent power.
✅ Cosine method: PF = cos φ from voltage-current phase angle.
✅ Measure kW, kVA with meters; estimate angle via V and I waveforms.
How Power Factor is Calculated - Calculating PF is crucial for understanding the efficiency of power use in AC circuits. In electrical systems, power factor (PF) represents the ratio between real power, which performs actual work, and apparent power (S), which is the total power supplied. A precise PF calculation can help optimize energy use, reduce costs, and enhance overall system performance. For a step-by-step overview, consult the how to calculate power factor guide to confirm each stage aligns with best practice.
Power Quality Analysis Training
Request a Free Power Quality Training Quotation
Understanding PF Components
To calculate PF, it’s essential first to understand the types of power involved: real power (active power), otherwise known as "P", reactive power (Q), and apparent power (S). Real power, measured in kilowatts (kW), is the power that does useful work. Reactive power, measured in kilovolt-amperes reactive (kVAR), is necessary for creating and sustaining magnetic fields, especially with inductive loads like motors or capacitive loads such as capacitors. Apparent power, expressed in kilovolt-amperes (kVA), combines both real and reactive power. A concise derivation is outlined in the power factor formula reference for quick review.
Test Your Knowledge About Power Quality!
Think you know Power Quality? Take our quick, interactive quiz and test your knowledge in minutes.
- Instantly see your results and score
- Identify strengths and areas for improvement
- Challenge yourself on real-world electrical topics
PF is the ratio of P to S, indicating how efficiently the electrical energy is used. The formula for PF is:
PF = P (kW) / S (kVA)
Practical examples in the power factor calculation article illustrate how different load types shift this ratio.
This ratio shows how much of the S is effectively converted into useful work, with a PF of 1 indicating perfect efficiency. In field audits, technicians often use the how to find power factor workflow to corroborate instrument readings.
The Process of Calculating PF
To calculate PF, you need measurements of both P and S. An analyzer or quality analyzer is typically used in electrical systems to capture these values accurately. A dedicated power factor meter streamlines this task by computing PF from real-time voltage and current.
Measure Real Power (kW): This is the actual power consumed by the system to perform work, like running machinery or lighting. Real power is what you aim to maximize within the limits of efficiency.
Measure Apparent Power (kVA): S is the product of the circuit’s voltage (V) and current (A). The equation for S in an AC circuit is:
kVA = Voltage (V) × Current (A)
When sizing equipment, the power factor calculator helps validate kVA values against measured kW and PF.
Calculate the PF: With P and S measured, PF can be calculated by dividing P by S:
PF = kW / kVA
Consider Phase Angle and Q:
In AC circuits, the phase angle between current and voltage affects the PF. Inductive loads, which create a lagging PF, result in a larger phase angle, increasing reactive power. This reactive power doesn’t perform useful work but influences the PF calculation by affecting the total apparent power. For remediation planning, the power factor correction formula provides capacitor sizing estimates that target a specified PF.
Why Power Factor Calculation Matters
A poor PF means higher S consumption, which can lead to inefficiencies and increased operational costs. Understanding how PF is calculated allows companies to implement PF correction measures, typically by adding capacitive loads to balance inductive loads. PF correction reduces the need for Q, thereby improving the ratio of real power to apparent power.
Improving Power Factor in Electrical Systems
Investing in PQ analyzers and implementing PF correction can help maintain a high PF, ensuring efficient usage and reducing costs. Proper correction methods, such as adding capacitors to counterbalance inductive loads, help improve PF and lower the overall electrical consumption.
Calculating PF accurately is essential for optimizing electricity consumption in AC circuits. By focusing on the ratio of P to S and understanding the effects of Q and phase angle, businesses can achieve more efficient energy use and reduce costs associated with poor PF.