Reactive Power Formula in AC Circuits
By R.W. Hurst, Editor
Power Quality Analysis Training
Our customized live online or in‑person group training can be delivered to your staff at your location.
- Live Online
- 12 hours Instructor-led
- Group Training Available
Reactive power (Q) is calculated using the formula: Q = V × I × sin(θ), where V is voltage, I is current, and θ is the phase angle. It is measured in VAR (volt-ampere reactive) and represents non-working power in AC systems.
What is a Reactive Power Formula?
The reactive power formula is Q = V × I × sin(φ), where Q represents the reactive power, V is the voltage, I is the current, and φ is the phase angle between the voltage and the current.
✅ Calculates power due to phase difference between voltage and current
✅ Helps assess efficiency in AC electrical systems
✅ Essential for sizing capacitors and power factor correction
Power Quality Analysis Training
Request a Free Power Quality Training Quotation
The reactive formula is Q = V × I × sin(φ), where Q represents the non-working energy, V is the voltage, I is the current, and φ is the phase angle between them. The correction factor is crucial in this equation, as it affects the amount of reactive flow required to sustain the circuit. Compensation techniques are used to balance this flow, while power factor correction enhances electrical efficiency, especially in induction machines. Understanding this relationship is essential for engineers and technicians to design, maintain, and operate efficient AC networks. To see how it fits into broader electrical theory, visit our Power Quality Channel.
In an AC system, this non-consumed flow sustains the magnetic and electric fields of inductors and capacitors. However, it doesn’t contribute to useful work like lighting or mechanical motion. Instead, it cycles between source and load, causing phase shifts in voltage and current. You can verify your calculations using our apparent power calculator to better size equipment or assess efficiency.
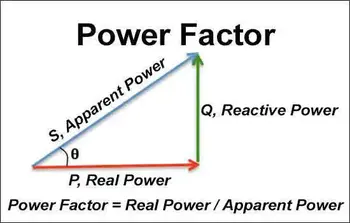
Reactive flow is measured in Volt-Amperes Reactive (VAR) or Kilovolt-Amperes Reactive (KVAR). Knowing this formula is essential for system analysis and maintaining reliable electrical delivery. This article explains the concept, how to calculate it in AC circuits, and why the correction factor matters. The relationship between apparent, reactive, and active output is best visualized using the power triangle.
Electricity Today T&D Magazine Subscribe for FREE
- Timely insights from industry experts
- Practical solutions T&D engineers
- Free access to every issue
Reactive Energy in AC Systems
In AC distribution, this form of electrical load flows cyclically without being consumed. It’s required to maintain the magnetic properties of key components like motors, transformers, and generators. Denoted by Q and measured in VAR or KVAR, it does not perform useful mechanical work. In perfect phase alignment, this flow is absent—but most real-world circuits exhibit either inductive or capacitive displacement.
Power Triangle
The triangle visually represents the relationship between active work, reactive flow, and total delivery. Active energy refers to what is converted into work, measured in watts (W) or kilowatts (kW). Reactive energy is what sustains fields, measured in VAR or KVAR. Apparent capacity is the combined effect of both, forming the hypotenuse of the triangle. The angle phi (φ) defines the ratio between real output and total delivery, known as the power factor.
Reactive Power Formula
The base formula is Q = V × I × sin(φ), where Q is the reactive component, V the voltage, I the current, and φ the phase angle. This angle—positive for lagging, negative for leading—is measured in degrees or radians. With known voltage, current, and power factor, Q can be calculated directly.
Reactive Power Calculation
In single-phase setups, voltage and current can be measured using standard meters, while φ is found via a phase meter or analyzer. In three-phase systems, average current and angle values are taken across all phases. See our guide on how to calculate power factor for a deeper dive into system efficiency.
For three-phase configurations, the formula becomes Q = √3 × V × I × sin(φ), where √3 accounts for the triangular configuration of phases. Learn how to enhance overall performance with power factor correction strategies, including automatic systems and capacitor banks.
KVAR Calculation
Sometimes, we may need to calculate the KVAR in an AC circuit. KVAR is simply the reactive power in Kilovolt-Amperes Reactive. To convert VAR to KVAR, we need to divide the VAR value by 1000. Therefore, the formula for calculating KVAR is Q (KVAR) = Q (VAR) / 1000.
Power Factor
The correction factor (or power factor) reflects efficiency and is defined as the ratio of active power to apparent power. A high value (near 1) indicates efficient use of supplied current. A low factor implies excess reactive load, causing waste. Power factor correction techniques can mitigate this through the use of capacitors.
Induction Motors
These machines rely on both active and reactive supply. The ratio between them defines the motor’s power factor. A low rating leads to overheating, inefficiency, and potential damage. Proper correction ensures smoother operation—read more in our motor power factor article.
Reactive Power Compensation
Too much non-working flow can result in voltage drops, losses, and equipment strain. Compensation devices like capacitors, inductors, and SVCs (Static VAR Compensators) are employed to restore system balance.
Related Pages