3 phase power formula
The 3 phase power formula calculates total electrical power using voltage, current, and power factor. It supports constant power in industrial applications and balanced phase systems across 120 degrees, ensuring efficiency in electrical engineering and power system design.
What is: “3 phase power formula”
The 3 phase power formula is used to calculate electrical power in three-phase systems, common in industrial and engineering applications.
✅ Calculates active and apparent power using voltage, current, and power factor
✅ Ensures constant power across 120-degree phase circuits
✅ Supports efficient power systems in industrial applications
Power Quality Analysis Training
Request a Free Power Quality Training Quotation
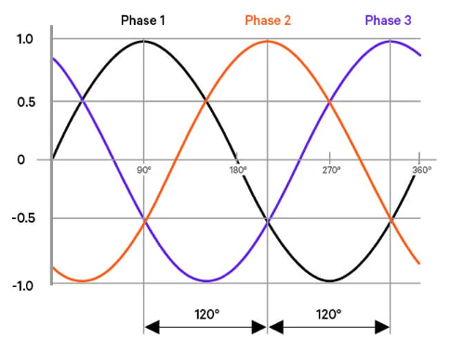
In electrical engineering, understanding the 3 phase power formula is fundamental for designing power systems used in industrial applications. Three‑phase systems consist of three alternating currents, each shifted by 120 degrees in phase angle relative to each other. This arrangement provides constant power transfer to loads, unlike single-phase systems, where power fluctuates each cycle.
The cornerstone is the relationship involving the square root of three (√3 ≈ 1.732). In a balanced three‑phase circuit, the line-to-neutral voltage (V_ln) is related to the line-to-line voltage (V_ll) by V_ll = √3 × V_ln =
This √3 factor arises because the three phasors are spaced by 120 degrees.
Phase power calculation
A single-phase circuit carries a portion of the load, and its phase power (active) is:
P_phase = V_phase × I_phase × pf
Where pf is the power factor (cos φ), accounting for phase displacement between current and voltage
Total power in three-phase
For total power delivered in a balanced 3-phase system, the formula is:
total power = √3 × V_ll × I_line × power factor pf
This yields the apparent power in VA; multiply by pf to get the active power in watts. In kilowatts (kW), divide by 1,000.
For a star (wye) configuration, you might also use:
total power = 3 × V_ln × I_line × pf
Active vs apparent power
In any system, active power (useful work) is:
P = VI cos φ
Apparent power (S) is:
S = VI
and power factor pf = P / S. In three phases:
S_total = √3 × V_ll × I_line
So active:
P_active = S_total × pf
Constant power and industrial benefits
Three-phase supplies constant power delivery due to overlapping phase currents that cancel fluctuations. This ensures the smooth operation of motors and generators in industrial applications. Compared to a single-phase power system, a three-phase system with equal V and I supplies approximately 1.732 times more electrical power.
Practical example
Consider a 208 V line‑to‑line three‑phase load drawing 20 A with pf of 0.8:
√3 × 208 × 20 × 0.8 ≈ 5,750 W (≈ 5.75 kW)
This shows how kilowatts (kw) are calculated using the 3 phase power formula.
Phase circuit vs total system
Each phase circuit sees V_ln and I_line; the three combined yield total power. In a delta configuration, each phase sees V_ll directly, while line currents differ: I_line = √3 × I_phase.
Why power factor and phase angle matter
The phase angle between voltage and current shifts with inductive or capacitive loads. That shift determines pf. In three-phase power factor correction, utilities or engineers aim for pf close to 1 to minimize losses and cost.
Relation to single-phase systems
In single-phase systems, the power formula is simply P = V × I × pf. By extending to three separate phases shifted by 120 degrees, you sum three times the phase power — or use the √3‑based formula — to arrive at total power for the system.
Common uses and summary
Three-phase power formulas are central to electrical power distribution, three-phase electrical machines, and power supplied by generators or grids. Engineers apply them in electrical engineering designs, especially in industrial applications where large motors and equipment demand constant power.
In summary, the key formulas:
-
Single phase: P = V × I × pf
Three-phase: P_total = √3 × V_ll × I_line × pf
or P_total = 3 × V_ln × I_line × pf
By incorporating active power, apparent power, power factor, and the square root of three, this unified framework supports precise phase power calculation in modern power systems and industrial engineering.
Related Articles
On-Site Training
Interested in cost effective, professional on-site electrical training?
We can present an Electrical Training Course to your electrical engineering and maintenance staff, on your premises, tailored to your specific equipment and requirements. Click on the link below to request a Free quotation.
