Delta to Wye Conversion

Delta to Wye conversion transforms a triangle-shaped (Δ) circuit into a Y-shaped network, improving grounding, balancing three-phase loads, and simplifying power system analysis. It’s essential for transformer design, circuit simplification, and safe energy distribution.

What is "Delta to Wye Conversion"?

Delta to Wye Conversion is the process of reconfiguring a three-phase electrical system to improve safety and functionality.

✅ Enhances grounding and fault protection

✅ Balances load distribution across phases

✅ Reduces transformer and equipment strain

Electrical Transformer Maintenance Training

Substation Maintenance Training

Request a Free Training Quotation

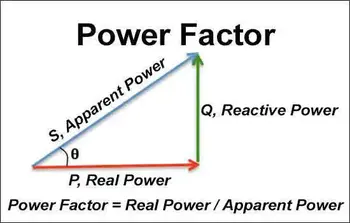
Understanding Delta and Wye Networks

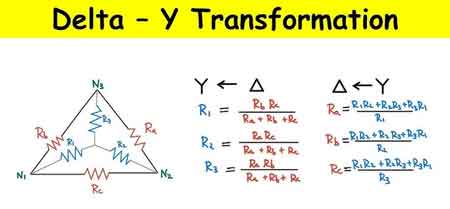
In a delta (Δ) network, three resistors—typically labelled R1, R2, and R3—are connected end-to-end in a triangular formation. Each corner of the triangle connects to a pair of nodes, making it a common configuration in older transformer and motor designs. By contrast, a wye (Y) network features three resistors—Ra, Rb, and Rc—connected to a single central point, with each resistor extending outward to a terminal. This structure is preferred in modern systems due to its ease of grounding and phase balancing. To fully grasp the implications of Delta to Wye conversion, see our detailed comparison of Delta vs Wye three-phase power configurations.

Conversion Formulas: Delta to Wye

To convert a delta network into a wye network, each wye resistor must represent the same electrical behavior as seen between the terminals of the original delta network. The following formulas provide the values for the wye resistors:

• Ra = (R2 × R3) / (R1 + R2 + R3)

• Rb = (R1 × R3) / (R1 + R2 + R3)

• Rc = (R1 × R2) / (R1 + R2 + R3)

These calculations ensure that the new Y-network responds identically in terms of resistance, making it ideal for simplifying otherwise difficult network analysis problems. Learn how Delta-Wye transformers operate and support load balancing in power systems in our guide on Delta Wye Transformer and Three Phase Power

Applications of Delta to Wye Conversion

This transformation is especially valuable in resistive network analysis, where converting a delta to a wye enables the easier application of series-parallel simplification methods. It plays a critical role in electrical circuit theory, filter design, and impedance matching. In power systems, delta wye transformers are commonly used to change voltage levels while providing a grounded neutral point, which enhances safety and stability.

Delta to Wye conversion also facilitates load balancing in three-phase systems, which is essential for preventing overheating and minimizing equipment wear. For utilities and industrial systems, this technique supports the design of fault-tolerant and energy-efficient electrical infrastructures. Discover how Delta to Wye configurations relate to voltage conversion in our article on the 3 Phase to Single Phase Transformer.

Mastering the Concept

While the math behind the conversion is straightforward, visualizing the structural changes between the two configurations can deepen understanding. Diagrams, animations, and interactive tools can demonstrate how the same electrical behavior is preserved through the transformation. Studying real-world examples—such as how transformers in a substation apply delta to wye logic—can further clarify the benefits and reinforce the technique’s practical value.

Understanding Delta to Wye conversion is not just a theoretical exercise—it’s a practical skill that enhances electrical design, supports maintenance work, and underpins reliable power system operation.

When analyzing complex resistor networks, Delta to Wye conversion is particularly useful because it allows engineers to simplify circuits into manageable combinations of series and parallel resistors between any pair of terminals. This simplification is essential for applying analytical techniques such as superposition theorems, which require linear circuit elements and straightforward configurations to isolate the effects of individual sources. By converting a delta network into an equivalent wye (or vice versa, depending on the desired analysis), one can more easily determine current and voltage distributions without altering the overall behavior of the circuit as seen from the outside terminals.

Related Pages

• Delta Wye Transformer
• 3 Phase to Single Phase Transformer
• Power Transformer Maintenance Training
• Substation Maintenance Training
• Utility Transformer Channel