Power Factor Calculation

Power Factor Calculation shows how to compute PF = kW ÷ kVA to gauge AC efficiency, phase angle, and reactive power. Learn formulas, examples, and capacitor correction to cut kVAR, reduce losses, and size equipment for motors and utility systems.

What is a Power Factor Calculation?

Power factor calculation is a core concept in electrical engineering that measures the relationship between real power, reactive power, and apparent power in AC circuits.

✅ Computes PF = kW/kVA to relate real power to apparent power in AC circuits

✅ Uses phase angle (cos φ) to quantify reactive power and efficiency losses

✅ Guides capacitor correction (kVAR) to reduce demand charges and size equipment

A high PF means electrical energy is being used effectively. A low PF indicates inefficiency, often caused by inductive loads such as motors or transformers. The PF is affected by the load type and can be improved through PF correction (PFC), commonly by installing capacitors. To fully understand PF, it’s important to explore the broader concept of power quality and how it impacts electrical system performance.

Power Factor Training

Power Quality Analysis Training

Request a Free Power Quality Training Quotation

Definition and Range of Power Factor

Power factor is the ratio of real power (watts) to apparent power (volt-amperes), ranging from 0 to 1. A PF of 1 (unity) means all supplied energy is doing useful work. Anything less than 1 means a portion of the supplied energy is wasted as reactive power.

Types of Loads and Their Effect on PF

• Resistive loads (e.g., incandescent lamps, heating elements) have a PF of 1 because they consume energy directly without storing energy.

• Inductive loads (e.g., motors, transformers) have a lagging PF below 1, as they store energy in magnetic fields.

• Capacitive loads can produce a leading PF, returning energy to the circuit.

In practice, most loads are mixed, so PF can vary widely. Utilities often set minimum PF targets (e.g., 0.9–0.95) and may charge penalties for low PF.

The Power Triangle

The power triangle shows how real, reactive, and apparent power are related:

• P (Real Power, kW) – power doing useful work

• Q (Reactive Power, kVAR) – power exchanged with inductive/capacitive components

• S (Apparent Power, kVA) – total supplied power

Since PF is calculated using both real and apparent power, knowing how to apply the apparent power formula is essential for accurate results.

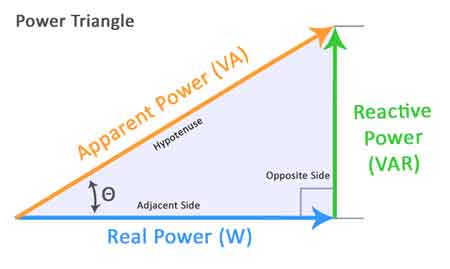
Power Triangle Diagram – Visual representation of the relationship between P, Q, and S in AC circuits, showing how PF is calculated using the phase angle (φ).

Formula:

PF = cos φ = P / S
sin φ = Q / S

In a diagram, P is the horizontal base, Q is the vertical side, and S is the hypotenuse. The angle φ between P and S is the phase difference between voltage and current.

Example Calculation

If P is 5 kW and S is 6 kVA:

PF = 5 ÷ 6 = 0.83

This means 83% of energy is useful work and 17% is reactive loss.

Load Factor vs. PF

Load factor measures average use of available energy over time:

Load Factor = Average Power ÷ Maximum Power

PF measures instantaneous efficiency. Together, they give a full picture of system performance.

Power Factor Correction (PFC)

The most common PFC method is adding capacitors in parallel with inductive loads to offset lagging Q. The required capacitance is:

C = Q / (2πfV²)

Where:

C = capacitance (F)
Q = reactive power (VAR)
f = frequency (Hz)
V = voltage (V)

Example:

For Q = 100 VAR, f = 60 Hz, V = 120 V:

C = 100 ÷ (2 × 3.14 × 60 × 120²) = 17.9 μF

Advanced Correction Methods

• Switched capacitor banks

• Synchronous condensers

• Static VAR compensators (SVC) or STATCOM

• Active harmonic filters

For step-by-step guidance, our how to calculate power factor page provides practical examples and explains how to use a power factor calculator.

Distortion PF and Harmonics

In modern electrical systems with non-linear loads (e.g., VFDs, computers, LED lighting), harmonics distort the current waveform. This lowers the true PF, which is:

True PF = Displacement PF ÷ √(1 + THDi²)

Where THDi is the total harmonic distortion of current. Correcting distortion PF often requires harmonic filters in addition to capacitors.

Accurate power factor calculation enables better energy efficiency, reduces utility penalties, and improves equipment performance. By combining PF analysis, load factor evaluation, and modern correction methods, facilities can achieve optimal electrical system performance.

Frequently Asked Questions

How do you calculate the PF?

The PF is calculated by dividing the P (measured in watts) by the S (measured in volt-amperes). The result is a number between 0 and 1, representing the PF. Improving PF often involves installing a power factor correction capacitor as part of a broader power factor correction strategy.

How are PF and load factor calculated?

The PF is calculated by dividing the P by the S, while the load factor is calculated by dividing the average energy by the maximum power. For motor-driven systems, our motor power factor guide explains the specific challenges and solutions for improving PF in industrial applications.

What is 0.9 power factor?

0.9 PF means that the circuit uses 90% of the supplied electricity effectively, and 10% is wasted. That would be considered poor PF. Therefore, it is a desirable PF for most electrical systems. Harmonic distortion can lower true PF, so learning about power quality and harmonics and using a power quality analyzer can help maintain system efficiency.

Related Pages

• Power Quality and Grounding Channel