Electrical Resistance Explained

Basic electricity refers to the fundamental concepts of electric charge, current, voltage, and resistance. It explains how electric circuits work, how energy flows, and how components like wires, batteries, and switches interact in homes, schools, and industries.

What is Basic Electricity?

Basic electricity refers to the foundational principles that explain how electric energy is generated, transmitted, and used in circuits. When an electric current flows through a conductor, it creates a magnetic field (or “flux”) around it.

✅ Explains current, voltage, resistance, and power in simple terms

✅ Describes how electric circuits operate and transfer energy

✅ Essential for understanding household wiring, batteries, and switches

Understanding the fundamentals of voltage is essential for grasping how electric circuits function — see our full explanation of voltage.

The strength of this magnetic field increases when the conductor is shaped into a coil with multiple turns. In electrical engineering, this coiled conductor is known as an inductor. If a steady direct current (DC) flows through the coil, it forms an electromagnet—an object with magnetic properties that can be switched on and off using a basic electrical switch.

Basic Electrical Theory

There are four basic electrical quantities that we need to know:

• Current

• Potential Difference (Voltage)

• Power

• Resistance

Electrical Current

Current is the movement of electric charge through a conductor. Each electron carries a charge of 1.6 × 10⁻¹⁹ coulombs—too small to measure individually—so we measure charge in groups called coulombs. When 1 coulomb of charge passes through a point in a circuit per second, the current is  1 ampere (A). Electric current is measured in amperes and is essential to the functioning of all electrical systems. Learn how voltage drop affects electrical performance and safety in residential and industrial systems. You can estimate losses in long-distance wiring with our easy-to-use voltage drop calculator. For step-by-step guidance on circuit loss calculations, explore the voltage drop formula explained clearly.

Potential Difference

Voltage, or potential difference, refers to the energy per unit charge in a circuit. It represents the work each charge can perform. Think of voltage as the electrical pressure that pushes electrons through a conductor. Higher voltage means more potential energy available to do work, such as lighting a bulb or powering a motor.

Power in a Circuit

Electrical power is the rate at which energy is used or transferred in a circuit. It can be calculated using the formula:

Power (W) = Voltage (V) × Current (A)

This equation is fundamental in both residential and industrial applications, from estimating energy usage to designing electrical systems.

Electrical Resistant Behaviour

Resistance is the opposition to the flow of electric current. It determines how much current will flow for a given voltage. Materials like copper have low resistance and conduct electricity well, while materials like rubber have high resistance and are used as insulators. Learn how voltage drop affects electrical performance and safety in residential and industrial systems.

Electromagnetic Induction

There’s a reciprocal relationship between electric current and magnetism. When a magnet is moved past a conductor at a right angle, it induces a voltage in the conductor—a principle known as electromagnetic induction. The polarity of the induced voltage depends on the direction and orientation of the magnetic field.

This effect becomes more noticeable when the conductor is formed into a coil. As the north pole of the magnet passes the coil, voltage is induced, and current flows. When the south pole passes, the induced voltage reverses polarity, and the current changes direction. This principle is the foundation of generator operation. You can estimate losses in long-distance wiring with our easy-to-use voltage drop calculator.

The Generator and the Sine Wave

In an electric generator, coils placed on opposite sides of a rotating magnet generate alternating current (AC). These voltages combine, doubling the output. For example, a 120-volt, 60-Hz generator creates a wave that oscillates from +169.7V to -169.7V.

This wave is called a sine wave because the voltage at any point corresponds to the sine of the magnet’s angle of rotation. The cycle repeats 60 times per second in North America (60 Hz), creating the household AC power we are familiar with. For step-by-step guidance on circuit loss calculations, explore the voltage drop formula explained clearly.

Forms of Electricity: AC and DC

Electricity exists in two major forms:

• Alternating Current (AC): The direction of current flow alternates regularly. AC electricity is used in power grids because it is easier to transmit over long distances and is compatible with devices such as transformers and capacitors.

• Direct Current (DC): The current flows steadily in one direction. DC is commonly used inside electronics and battery-powered devices. Unlike AC, the voltage remains constant, making it easy to measure with a DC voltmeter.

AC – Alternating Current

Alternating current is the most common form of electricity used in homes, businesses, and utilities. It alternates direction 50–60 times per second, depending on the region. AC is generated by AC generators and is favored for its ability to change voltage levels easily, making it efficient for transmission over long distances. Sudden dips in power can disrupt equipment — find out what causes voltage sag and how to prevent it.

DC – Direct Current

Direct current flows continuously in one direction. Because its voltage is steady or changes very slowly, it’s easy to measure. It is used in battery-powered systems and internal electronic circuits. Unlike AC, DC cannot be easily stepped up or down in voltage without the use of complex circuitry.

When calculating AC power, engineers use RMS (Root Mean Square) voltage, which gives an effective value comparable to DC. For example, 120V AC RMS is equivalent in power to 120V DC, despite the AC waveform's variations. Discover how water and electricity interact, including safety considerations and risks in common environments.

Transformers and Induction

Transformers, built using coiled wires around iron cores, rely on electromagnetic induction. When AC flows through the primary coil, it creates a changing magnetic field that induces a voltage in the secondary coil. This allows voltage to be stepped up or down for different uses, such as high-voltage transmission or low-voltage device operation.

Atoms, Electrons, and Electric Charge

To fully grasp electricity, it’s essential to understand atomic structure. All matter is made up of atoms, which contain a nucleus of protons (positive) and neutrons (neutral), surrounded by orbiting electrons (negative). The outermost electrons—called valence electrons—can be knocked loose by energy, creating an electric current.

When electrons leave an atom, it becomes positively charged. This movement of charge is the essence of electricity. The ability of atoms to gain or lose electrons determines whether a material is a conductor (like copper) or an insulator (like plastic).

Electrical Charge and Attraction

One universal rule in electricity and magnetism is that like charges repel and opposite charges attract. A positively charged object will attract a negatively charged one. This principle governs everything from how circuits function to how magnetic fields interact with conductors. To understand how energy use is measured over time, read our overview of the watthour meter and its function.

Related Articles

• Electricity Fundamentals

• Electricity Questions

• Electricity History

Wattmeters measure electrical power in watts, monitoring energy use in industrial power systems. They provide accurate active power readings for efficiency and load management, utilizing voltage and current measurements to achieve precise results.

What are Wattmeters?

Wattmeters are instruments used to measure electrical power. They:

✅ Measure active electrical power in watts for various applications.

✅ Are used in industrial, commercial, and residential energy monitoring.

✅ Help optimize efficiency, manage loads, and ensure system safety.

A wattmeter measures instantaneous (or short-term) electrical power in watts, while a watthour meter accumulates that power over time and reports energy used (e.g. in kWh). Energy meters and smart meters extend this concept by recording consumption continuously for billing, load analysis, and energy audits.

Working Principle of Wattmeters

Electrical power is calculated using the formula:

P = E × I

Where:

• P = Power in watts

• E = Voltage in volts

• I = Current in amperes

In DC circuits, watts are sometimes expressed as volt-amperes (VA). In AC circuits, wattmeters measure true (or active) power, taking into account the power factor to compensate for phase differences between voltage and current. Unlike reactive power (measured in kvar) or apparent power (measured in kVA), active power is the usable portion that does real work. This relationship is often represented in the power triangle, where vector analysis explains how apparent, reactive, and active power interact.

Construction and Internal Components

A typical wattmeter consists of two main coil assemblies:

1. Current Coil (CC)

   • Heavy-gauge copper wire with low resistance.

   • Connected in series with the load to carry the circuit current.

2. Voltage Coil (VC)

   • Fine-gauge wire with high resistance.

   • Connected in parallel with the load to measure voltage.

The electrodynamometer, commonly referred to as a dynamometer wattmeter, is a classic analog device that operates on the principle of a motor. The interaction between the magnetic fields of the current and voltage coils produces a torque proportional to the power, causing the pointer to move over a calibrated scale. Understanding wattmeter principles is a foundation of basic electricity training, helping learners connect theory to practical power measurement.

Figure 1 – Construction of a dynamometer wattmeter showing current and voltage coil arrangement.

Types of Wattmeters

• Analog/Dynamometer – Durable, reliable, suited for laboratory and field measurements.

• Digital – Higher accuracy, data logging, and integration with monitoring systems.

• Clamp-on  – Measure power without breaking the circuit, ideal for quick diagnostics.

• Specialized  – Designed for RF power, audio power, or other niche applications.

In three-phase systems, wattmeters are often applied in accordance with Blondel’s theorem, which specifies the number of measurement elements required in multi-phase circuits. They are frequently used in conjunction with 3 phase electricity concepts to ensure balanced load distribution and optimal system efficiency.

Fig. 2. Power can be measured with a voltmeter and an ammeter.

Measuring Power in DC and AC Circuits

In DC circuits, power measurement can be as simple as multiplying voltage and current readings from separate meters.

Example:

If a circuit operates at 117 V DC and draws 1 A, the power is:

P = 117 × 1 = 117 W

In AC systems, especially with reactive or distorted loads, a wattmeter is essential because voltage and current may not be in phase. The device automatically accounts for the phase angle, providing accurate true power readings. Advanced digital wattmeters also compensate for harmonic distortion and poor waveform quality, providing more reliable measurements than older analog designs.

By measuring energy transfer in circuits, they also relate to other power measurement instruments such as ammeters, voltmeters, and multimeters, which measure supporting parameters needed for complete electrical analysis. Accurate wattmeter readings are crucial for diagnosing performance issues in 3-phase power networks, where the relationships between voltage and current are critical. By measuring energy transfer in circuits, they help explain fundamental laws of electromagnetism, such as Ampère’s Law, which underpins the interaction between current and magnetic fields.

Fig. 2. Power can be measured with a voltmeter and an ammeter.

Practical Examples and Load Considerations

A household iron may consume 1000 W, drawing 8.55 A at 117 V.

A large heater may draw 2000 W, or 17.1 A, potentially overloading a 15 A breaker.

In industrial settings, watt meters help prevent equipment overloading, reduce downtime, and improve energy efficiency.

Modern Wattmeter Applications

Today’s wattmeters are often part of smart energy monitoring systems that:

• Track energy consumption over time.

• Integrate with SCADA and IoT platforms.

• Enable predictive maintenance through power trend analysis.

• Support compliance with energy efficiency regulations.

Accuracy, Standards, and Advanced Considerations

Measurement accuracy is a crucial factor in determining wattmeter performance. Devices are often classified by a class of accuracy, with error limits defined by international standards such as IEC, ANSI, or IEEE. Regular calibration and testing procedures ensure watt meters continue to deliver reliable results in both laboratory and field conditions.

Modern digital watt meters feature true RMS measurement, which accurately captures distorted waveforms caused by nonlinear loads. This is especially important in power systems where harmonic distortion is present. In commercial and industrial environments, accurate wattmeter data support energy audits, load analysis, and regulatory compliance, making them indispensable tools for engineers and facility managers. Wattmeter usage is closely linked to the fundamentals of electrical energy, enabling precise monitoring for efficiency and cost control.

Key Advantages of Wattmeters

• Accurate real-time power measurement.

• Enhanced energy management and cost savings.

• Improved system reliability through overload prevention.

• Compatibility with both AC and DC systems.

Wattmeters remain a vital tool for measuring and managing electrical power. Whether in a simple residential circuit, a commercial energy audit, or a high-tech industrial monitoring system, they ensure that electrical systems run efficiently, safely, and cost-effectively. As technology advances, digital and networked wattmeters continue to expand their role, integrating into smart grids and energy-optimized infrastructures. 

Related Articles

• Electricity Fundamentals

• Electricity Questions

• Electricity History

Watt’s Law defines the relationship between power (watts), voltage (volts), and current (amps): Power = Voltage × Current. It’s used in electrical calculations to determine energy usage, system efficiency, and safe equipment ratings in both residential and industrial systems.

What is: Watt’s Law?

Watt’s Law is a fundamental principle in electrical engineering:

✅ Calculates electrical power as the product of voltage and current

✅ Helps design efficient and safe electrical systems

✅ Used in both residential and industrial applications

Watt’s Law is a fundamental principle in electrical engineering that defines the relationship between power, voltage, and current in an electrical circuit. James Watt invented the law. It states that the power (measured in watts) of an electrical device is equal to the product of the voltage (measured in volts) and the current (measured in amperes) flowing through it. In other words, the watt's law formula is expressed as: Power = Voltage × Current. This simple equation is essential for understanding how electrical components consume and distribute energy in a circuit. 

For example, consider a light bulb connected to an electrical circuit. The electrical potential (voltage) pushes the electric charge through the filament of the bulb, creating a flow of electrons (current). As the electrons flow, they generate heat and light, representing the bulb’s power in a circuit. By knowing the voltage and current, you can easily calculate the power output of the bulb. The wattage of the bulb indicates the energy consumed per second.

Practical applications of this formula are vast. This equation is especially useful in designing safe and efficient electrical systems. For instance, designing the wiring for both small devices and large power systems requires a thorough understanding of the relationship between voltage, current, and power. The formula helps ensure that systems are capable of delivering the required energy without causing failures or inefficiencies.

Ohm’s Law and this principle are often used together in electrical engineering. While power focuses on the relationship between voltage and current, Ohm’s Law deals with the relationship between voltage, current, and resistance (measured in ohms). Ohm’s Law states that voltage equals current multiplied by resistance (Voltage = Current × Resistance). By combining Ohm’s Law and this power equation, you can analyze an electrical system more comprehensively. For example, if you know the voltage and resistance in a circuit, you can calculate the current and then determine the power in the circuit. To fully understand Watt's Law, it helps to explore how voltage and current electricity interact in a typical electrical circuit.

Georg Simon Ohm – German physicist and mathematician (1787–1854), known for Ohm's Law, relating voltage, current, and resistance.

What is Watt's Law and how is it used in electrical circuits?

Watt’s Law is a fundamental principle in electrical engineering that defines the relationship between power, voltage, and current in an electrical circuit. The formula is expressed as:

Power (Watts) = Voltage (Volts) × Current (Amperes)

In simpler terms, Watt’s Law states that the electrical power consumed by a device (measured in watts) is the product of the electrical potential difference (voltage) and the current flowing through the circuit. Accurate calculations using Watt’s Law often require a voltage-drop calculator to account for line losses in long-distance wiring. Comparing voltage drop and voltage sag conditions illustrates how slight changes in voltage can have a substantial impact on power output.

James Watt – Scottish inventor and mechanical engineer (1736–1819), whose improvements to the steam engine led to the naming of the watt (unit of power).

How is it used? Watt’s Law is widely used to determine the amount of power an electrical device or system consumes. This is especially important for designing electrical circuits, optimizing power distribution, and ensuring the efficiency of devices. Here are a few examples of how it’s applied:

• Electrical Circuit Design: Engineers use it to calculate the power consumption of devices and ensure that circuits can handle the expected electrical load. This helps prevent overloads and ensures that the wiring is safe.

• Power Output Calculations: Using this formula, you can calculate the power output of a generator, appliance, or device, enabling you to match the right components to your system's requirements.

• Energy Efficiency: Understanding power consumption in appliances and devices helps consumers make informed choices, such as selecting energy-efficient options. Devices like wattmeters and watthour meters measure power and energy usage based directly on the principles of Watt’s Law. For a deeper look at how devices like ammeters help measure current, see how their readings plug directly into Watt’s Law calculations.

How is Watt's Law different from Ohm's Law?

Watt’s Law and Ohm’s Law are both fundamental principles in electrical engineering, but they deal with different aspects of electrical systems:

• Watt’s Law defines the relationship between power, voltage, and current. It focuses on the amount of energy used by a device in a given circuit. The formula is:

           Power = Voltage × Current

• Ohm’s Law defines the relationship between voltage, current, and resistance in a circuit. Ohm’s Law explains how the current is affected by the voltage and the resistance present in the circuit. The formula for Ohm’s Law is:

            Voltage = Current × Resistance

Key Differences:

• Focus: It focuses on power, while Ohm’s Law focuses on the flow of electricity in a circuit, particularly how resistance affects current.

• Watt’s Law is used to determine the amount of power a device is consuming. Ohm’s Law, on the other hand, is used to calculate current, voltage, or resistance in a circuit depending on the other known variables.

• Applications: It is applied when designing systems that require power management, such as calculating the power output or efficiency of devices. Ohm’s Law is used more in analyzing how current behaves in a circuit when different resistive elements are present.

By combining both laws, electrical engineers can gain a comprehensive understanding of how electrical systems function, ensuring that devices operate efficiently and safely. When used with Ohm’s Law, Watt's Law enables engineers to analyze both energy consumption and electrical resistance.

One key area of application is in energy consumption. By understanding the voltage and current values for a specific device, engineers can monitor the amount of energy the device consumes. This is especially important for managing energy usage in homes, businesses, and power systems. By applying the formula, you can identify inefficient devices and make more informed decisions about energy efficiency.

In renewable energy systems, such as solar panels and wind turbines, this principle plays a critical role in optimizing energy output. Engineers use the formula to calculate how much electrical energy is being generated and distributed. This is crucial for ensuring that power systems operate efficiently and minimize excess energy loss.

Another practical application of this formula is in the automotive industry. It is used to design vehicle charging systems and battery technologies. For example, electric vehicle (EV) charging stations depend on understanding voltage, current, and power to ensure efficient charging times. Engineers use the equation to calculate the charging capacity required for EV batteries, helping to create optimal charging solutions.

In large facilities like data centers, this Watt’s Law formula is used to ensure power distribution is efficient. By applying the relationship between power, voltage, and current, engineers can effectively manage power systems, thereby reducing energy consumption and operational costs. Proper energy management in data centers is crucial, as high power usage can result in significant energy costs.

This power formula is indispensable for electrical engineers and technicians. The applications of Watt’s Law extend across various industries and are utilized in everything from designing power system wiring to developing renewable energy technologies. By combining Ohm’s Law and this principle, electrical engineers can optimize the performance of electrical components, ensuring energy efficiency and system reliability. Understanding the role of a resistor in a circuit can reveal how power is dissipated as heat, a key concept derived from Watt’s Law.

Finally, visual tools like the Watt's Law triangle are often used to simplify the application of this principle, helping both professionals and students understand how to apply the formula. As technology advances and energy demands grow, this formula remains a key element in electrical engineering, guiding the development of more efficient systems for the future.

Related Articles

• Electricity Fundamentals

• Electricity Questions

• Electricity History

Electrical resistance is the opposition to the flow of electric current in a material. It is measured in ohms (Ω) and depends on the conductor’s length, thickness, material, and temperature.

What is Electrical Resistance?

Electrical resistance is a fundamental concept in engineering that defines how much a material opposes the flow of electric current. Measured in ohms (Ω), resistance (Ω) plays a crucial role in circuit design, power distribution, and electronic applications.

✅ Measured in ohms (Ω) and calculated using Ohm’s Law

✅ Influenced by material, length, area, and temperature

✅ Key factor in circuit safety, design, and energy loss

Think of electricity moving like water through a pipe. If the pipe is narrow or obstructed, less water flows through it. Similarly, in a wire or conductor, certain materials make it harder for electrons to move freely. This obstruction results in energy loss, often seen as heat.

The ease or difficulty of electric charge movement depends on the conductivity of a material. Metals like copper allow current to flow easily, while rubber or glass inhibit it entirely. This behavior plays a key role in how systems are designed and protected. Discover how resistors are used in circuits to manage voltage and protect components by providing controlled resistance.

Electrical Resistance – Example Values by Material/Component

Electrical Resistance Definition

Several factors affecting electrical resistance include the type of material, temperature, and the dimensions of the conductor. When an electric charge moves through a material, its ease of flow depends on the material’s conductivity. A high-conductivity material allows charges to move more freely, resulting in lower resistance. The resistance of a conductor increases with its length and decreases with its cross-sectional area. Therefore, the resistance of a wire is directly related to both its physical properties and the material from which it is made. The resistance of a conductor depends heavily on its length and cross-sectional area, as outlined in our resistance formula breakdown.

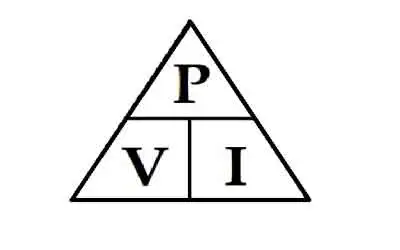
This opposing property is quantified using Ohm’s Law:

R = V / I

Where:

• R is the resistive value in ohms

• V is voltage (volts)

• I is current (amperes)

Another useful expression involves material properties:

R = ρ × (L / A)

Where:

• ρ is resistivity (material-specific)

• L is length

• A is cross-sectional area

These formulas show that the longer or thinner the conductor, the harder it is for current to move through it.

Unit of Electrical Resistance – The Ohm (Ω)

The ohm is the SI unit of resistance, named after German physicist Georg Ohm. One ohm is defined as the resistance between two points of a conductor when a potential difference of one volt causes a current of one ampere to flow.

Common multiples:

• kΩ (kilo-ohm) = 1,000 ohms

• MΩ (mega-ohm) = 1,000,000 ohms

Resistance can be measured using a multimeter, and is especially important in designing and troubleshooting power  and electronic circuits. To understand how voltage and resistance interact in a circuit, see our guide on Ohm’s Law.

Ohm’s Law and Circuit Function

Ohm’s Law helps us understand how voltage, current, and resistance relate. For example:

• Increase the resistive load, and current drops.

• Increase voltage with fixed resistance, and current rises.

These principles help control energy flow, prevent overloads, and design efficient systems.

Measuring and Expressing Opposition

The ohm (Ω) is the standard unit used to quantify this phenomenon. One ohm means that a current of one ampere flows when one volt is applied. Components with fixed values, like resistors, are labelled accordingly—e.g., 100 Ω, 1 kΩ, or 1 MΩ.

To measure the current-limiting capacity of a material, a digital multimeter is used. It applies a small voltage and calculates the resulting current flow to determine the opposition level. If you're working with different wire types, explore the unit of electrical resistance for conversion insights and resistance ranges.

Real-World Examples of Resistance

• Heating Elements: Toasters, ovens, and electric heaters utilize high-resistance materials, such as nichrome wire.

• Power Transmission: Long-distance wires are designed with low resistance to reduce energy loss as heat.

• Electronic Components: Resistors regulate current in circuits, protecting components from overload.

For real-world scenarios involving current flow, our article on voltage drop explains how resistance affects electrical efficiency over distance.

Factors Affecting Electrical Resistance

• The resistance of a conductor depends on:

  • Material – copper vs. aluminum vs. nichrome

  • Length – longer wires restrict current more

  • Thickness – wider wires allow easier flow

  • Temperature – many materials resist current more when heated

  Thus, the resistance of a wire can vary dramatically depending on where and how it’s used. Materials with high conductivity (like silver or copper) allow electrons to move with minimal restriction, whereas poor conductors like rubber greatly hinder charge movement.

Superconductors – Zero Resistance?

In some materials, when cooled to extremely low temperatures, resistance drops to zero. These superconductors enable electricity to flow without energy loss, but their use is limited to specialized fields, such as MRI machines or experimental power lines, due to cost and cooling requirements.

Frequently Asked Questions

What causes electrical resistance?

It results from collisions between electrons and atoms in a conductor, which convert energy into heat.

What is the formula for calculating it?

 R = V/I or R = ρ × (L / A)

How is it measured?

With a multimeter in ohms (Ω), using a small test voltage and measuring current. Learn how instruments like a digital multimeter are used to measure opposition to current flow in electrical systems.

Why is this concept important?

It controls current flow, prevents damage, and enables functions like heating or dimming.

Can resistance ever be zero?

Yes—in superconductors under specific extreme conditions.

Electrical resistance is a foundational concept in understanding how electricity behaves in materials and systems. From household wiring to high-voltage power lines and sensitive electronics, it plays a crucial role in determining safety, efficiency, and performance. For a broader view on electric flow and material response, read about electrical conductivity and current electricity.

Related Articles

• Electricity Fundamentals

• Electricity Questions

• Electricity History

Electricity and magnetism are interconnected forces forming electromagnetism, which explains electric currents, magnetic fields, and their interactions. These principles power motors, generators, transformers, and more in modern electrical and magnetic systems.

What is: "Electricity and Magnetism"

Electricity and magnetism are fundamental forces in physics that form the basis of electromagnetism.

✅ Describe how electric charges and magnetic fields interact in nature and technology

✅ Underlie the function of motors, transformers, and generators

✅ Explain current flow, induction, and electromagnetic waves

Electricity - What is it?

Electricity is a form of energy that is transmitted through copper conductor wire to power the operation of electrical machines and devices, including industrial, commercial, institutional, and residential lighting, electric motors, electrical transformers, communications networks, home appliances, and electronics.

When charged particles flow through the conductor, we call it "current electricity". This is because when the charged particles flow through wires, electricity also flows. We know that current means the flow of anything in a particular direction. For example, the flow of water. Similarly, the flow of electricity in a specific direction is referred to as an electric current. The interplay of charge, field, and force is explored in what is electric load, covering how power is delivered in electromagnetic systems.

When an electric current flows, it produces a magnetic field, a concept closely tied to Faraday's Law of Induction, which underpins much of modern electrical engineering.

Magnetism  - What is it?

Magnetism is a type of attractive or repulsive force that acts up to certain distance at the speed of light. The distance up to which this attractive or repulsive force acts is called a "magnetic field". Magnetism is caused by the moving electric charges (especially electrons). When two magnetic materials are placed close to each other, they experience an attractive or repulsive force. To understand magnetic field strength and units, our magnetic induction basics in induction page discusses flux and Teslas.

What is the relationship between electricity and magnetism?

In the early days, scientists believed that there were two uniquely separate forces. However, James Clerk Maxwell proved that these two separate forces were actually interrelated.

In 1820, Hans Christian Ørsted observed a surprising phenomenon: when he switched on the battery from which the electric current was flowing, the compass needle moved away from the north pole. After this experiment, he concluded that the electric current flowing through the wire produces a magnetic field.

Electricity and magnetism are closely related to each other. The electric current flowing through the wire produces a circular magnetic field outside the wire. The direction (clockwise or counterclockwise) of this magnetic field depends on the direction of the electric current.

Similarly, a changing magnetic field generates an electric current in a wire or conductor. The relationship between them is called electromagnetism.

Electricity and magnetism are interesting aspects of electrical sciences. We are familiar with the phenomenon of static cling in our everyday lives - when two objects, such as a piece of Saran wrap and a wool sweater, are rubbed together, they cling.

One feature of this that we don't encounter too often is static "repulsion" - if each piece of Saran wrap is rubbed on the wool sweater, then the pieces of Saran wrap will repel when brought near each other. These phenomena are interpreted in terms of the objects acquiring an electric charge, which has the following features:

• There are two types of charge, which by convention are labelled positive and negative.

• Like charges repel, and unlike charges attract.

• All objects may have a charge equal to an integral number of a basic unit of charge.

• Charge is never created or destroyed.

To explore how electric and magnetic forces interact at a distance, see what is static electricityis, which includes examples like static cling and repulsion.

Electric Fields

A convenient concept for describing these electric current and magnetic current forces is that of electric field currents. Imagine that we have a fixed distribution of charges, such as on the plate below, and bring a test charge Q into the vicinity of this distribution.

Fig. 1 Test charge in the presence of a fixed charge distribution

This charge will experience a force due to the presence of the other charges. One defines the electric field of the charge distribution as:

The electric field is a property of this fixed charge distribution; the force on a different charge Q' at the same point would be given by the product of the charge Q' and the same electric field. Note that the electric field at Q is always in the same direction as the electric force.

Because the force on a charge depends on the magnitude of the charges involved and the distances separating them, the electric field varies from point to point, both in magnitude and direction.

By convention, the direction of the electric field at a point is the direction of the force on a positive test charge placed at that point. An example of the electric field due to a positive point charge is given below. 

Fig. 2: Electric field lines of a positive charge

Power and Magnetic Fields

A phenomenon apparently unrelated to power is electromagnetic fields. We are familiar with these forces through the interaction of compasses with the Earth's magnetic field, or the use of fridge magnets or magnets on children's toys. Magnetic forces are explained in terms very similar to those used for electric forces:

• There are two types of magnetic poles, conventionally called North and South
• Like poles repel, and opposite poles attract

However, this attraction differs from electric power in one important aspect:

• Unlike electric charges, magnetic poles always occur in North-South pairs; there are no magnetic monopoles.

Later on we will see at the atomic level why this is so.

As in the case of electric charges, it is convenient to introduce the concept of a magnetic field in describing the action of magnetic forces. Magnetic field lines for a bar magnet are pictured below.

Fig. 3: Magnetic field lines of a bar magnet

One can interpret these lines as indicating the direction that a compass needle will point if placed at that position.

The strength of magnetic fields is measured in units of Teslas (T). One tesla is actually a relatively strong field - the earth's magnetic field is of the order of 0.0001 T.

Magnetic Forces On Moving Charges

One basic feature is that, in the vicinity of a magnetic field, a moving charge will experience a force. Interestingly, the force on the charged particle is always perpendicular to the direction it is moving. Thus, magnetic forces cause charged particles to change their direction of motion, but they do not change the speed of the particle.

This property is utilized in high-energy particle accelerators to focus beams of particles, which ultimately collide with targets to produce new particles, including gamma rays and radio waves.

Another way to understand these forces of electricity and magnetism is to realize that if the force is perpendicular to the motion, then no work is done. Hence, these forces do no work on charged particles and cannot increase their kinetic energy.

If a charged particle moves through a constant magnetic field, its speed stays the same, but its direction is constantly changing. A device that utilizes this property is the mass spectrometer, which is used to identify elements. A basic mass spectrometer is pictured below.

Figure 4: Mass spectrometer

In this device, a beam of charged particles (ions) enters a region of a magnetic field, where they experience a force and are bent in a circular path. The amount of bending depends on the mass (and charge) of the particle, and by measuring this amount one can infer the type of particle that is present by comparing it to the bending of known elements.

Magnet Power From Electric Power

A connection was discovered (accidentally) by Orsted over 100 years ago, when he noticed that a compass needle is deflected when brought into the vicinity of a current-carrying wire. Thus, currents induce magnetic fields in their vicinity. An electromagnet is simply a coil of wires which, when a current is passed through, generates a magnetic field, as below.

Figure 5: Electromagnet

Another example is in an atom, where an electron is a charge that moves around the nucleus. In effect, it forms a current loop, and hence, a magnetic field may be associated with an individual atom. It is this basic property which is believed to be the origin of the magnetic properties of various types of materials found in nature.

Maxwell's equations (also known as Maxwell's theory) are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, which deals with electromagnetic radiation, electromagnetic waves, and electromagnetic force.  For a deeper understanding of the magnetic effects of electrical current, our article on electromagnetic induction explains how magnetic fields can generate electricity in conductors.

Related Articles

• Electricity Fundamentals

• Electricity Questions

• Electricity History