Voltage Drop Formula

Types of electricity include static electricity and current electricity, which flows as direct current (DC) or alternating current (AC). Electricity can be generated from various sources, including solar, wind, and hydro, but all supply either static or current electricity.

What are the Types of Electricity?

There are two types of electricity: Static Electricity and Current Electricity.

✅ Static electricity results from the buildup of electric charges.

✅ Current electricity includes alternating (AC) and direct (DC) flow.

Static Electricity is made by rubbing together two or more objects, creating friction, while Current electricity is the flow of electric charge across an electrical field.

Static Electricity

Static electricity is when electrical charges build up on the surface of a material. It is usually caused by rubbing materials together. The result of a build-up of static electricity is that objects may be attracted to each other or may even cause a spark to jump from one to the other. For Example, rub a balloon on a wool and hold it up to the wall.

Before rubbing, like all materials, the balloons and the wool sweater have a neutral charge. This is because they each have an equal number of positively charged subatomic particles (protons) and negatively charged subatomic particles (electrons). When you rub the balloon with the wool sweater, electrons are transferred from the wool to the rubber because of differences in the attraction of the two materials for electrons. The balloon becomes negatively charged because it gains electrons from the wool, and the wool becomes positively charged because it loses electrons.

Current Electricity

Current is the rate of flow of electrons. The movement of electrons produces it, and it is measured in amperes. Unlike static electricity, current electricity must flow through a conductor, usually copper wire. Electricity is similar to the flow of water in a river. The river flows from one spot to another, and the speed of the current determines the speed at which it moves. With electricity, current is a measure of the amount of energy transferred over a period of time. That energy is referred to as an electron flow. One of the results of the current is the heating of the conductor. When an electric stove heats up, it's because of the flow of current.

There are various sources of current electricity, including the chemical reactions that occur in a battery. The most common source is the generator. A simple generator produces electricity when a coil of copper turns inside a magnetic field. In a power plant, electromagnets spinning inside many coils of copper wire generate vast quantities of electricity.

There are two main kinds of electric current. Direct (DC) and Alternating (AC). It's easy to remember. Direct current is similar to the energy you obtain from a battery. Alternating current is like the plugs in the wall. The big difference between the two is that DC is a flow of energy, while AC can turn on and off. AC reverses the direction of the electrons.

Related Articles

• Electricity Fundamentals

• Electricity Questions

• Electricity History

Kirchhoff's Law, comprising the Current Law (KCL) and Voltage Law (KVL), governs electrical circuits by ensuring charge conservation and energy balance, essential for analyzing current flow, voltage drops, and network behaviour.

What is Kirchhoff's Law?

Kirchhoff's law is an essential principle in the analysis of electrical circuits, enabling a comprehensive understanding of the behaviour of complex circuits.

✅ Defines relationships between currents and voltages in electrical circuits

✅ Ensures conservation of charge (KCL) and energy (KVL) in networks

✅ Essential for analyzing and solving complex circuit problems

It consists of two fundamental rules, Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL), which are intrinsically linked to other electricity laws, such as Ohm's law.  Kirchhoff’s Law works closely with Ohm’s Law Formula to calculate voltage drops, currents, and resistance in electrical networks.

Kirchhoff's Current Law (KCL) - Also known as the first Kirchhoff's law or Kirchhoff's junction rule, KCL states that the sum of the currents entering a junction in a circuit is equal to the sum of the currents leaving the junction. Mathematically, it can be expressed as:

ΣI_in = ΣI_out

KCL is based on the principle of the conservation of charge, asserting that charge can neither be created nor destroyed. In practical terms, KCL means that, at any given point in a circuit, the total current entering must equal the total current leaving, ensuring a continuous flow of electric charge. Understanding Basic Electricity provides the foundation for applying Kirchhoff’s Current Law and Voltage Law to real-world circuit analysis.

Kirchhoff's Voltage Law (KVL) - Also known as the second Kirchhoff's law or Kirchhoff's loop rule, KVL states that the sum of the voltage gains and losses (potential differences) around any closed loop in a circuit is zero. Mathematically, it can be expressed as:
ΣV_rise = ΣV_drop

KVL is based on the principle of the conservation of energy, indicating that energy cannot be created or destroyed but can only be converted from one form to another. In electrical circuits, KVL implies that the total voltage supplied in a loop equals the total voltage drop across all components, ensuring that energy is conserved. Accurate circuit calculations require a clear grasp of Electrical Resistance and how it impacts voltage distribution across components.

Relation to Other Electricity Laws

The most significant connection between Kirchhoff's and other electricity laws is Ohm's law, which defines the relationship between voltage, current, and resistance in an electrical circuit. Ohm's law can be expressed as:

V = IR

When analyzing a circuit using Kirchhoff's laws, Ohm's law is often employed to calculate unknown quantities such as voltage drops, currents, or resistance values. By combining Kirchhoff's laws with Ohm's law, a complete understanding of the behaviour of electrical circuits can be achieved, facilitating efficient design, troubleshooting, and optimization. Applying Kirchhoff’s principles is easier when you understand key Electrical Terms used in engineering and troubleshooting.

History

Gustav Robert Kirchhoff, a German physicist, made significant contributions to understanding electrical circuits by establishing two fundamental laws: Kirchhoff's Voltage Law (KVL) and Kirchhoff's Current Law (KCL). These laws are essential tools for circuit analysis, enabling engineers to design and troubleshoot electrical networks efficiently. In addition to resistance, Capacitance plays a vital role in determining circuit behavior, especially in AC systems.

KVL, also known as the loop rule, states that the algebraic sum of all the voltages around a closed loop equals zero. This principle is derived from the conservation of energy, which ensures that no energy is lost within a closed system. In essence, KVL states that the energy supplied to a circuit is equal to the energy consumed by the components in that circuit. Therefore, when solving problems using KVL, it is essential to consider voltage drops across resistive elements like resistors and voltage rises due to sources like batteries or generators.

On the other hand, KCL, or the junction rule, states that the algebraic sum of currents entering a junction (node) in a circuit is equal to the sum of currents leaving the same junction. This law is a consequence of the conservation of charge, which posits that charge cannot be created or destroyed within an electrical circuit. KCL ensures that the total charge entering and leaving a node remains constant, with the currents (I1, I2, I3, I4, I5) balancing each other. Knowledge of Voltage Drop is essential when using KVL to assess energy losses in electrical circuits.

The significance of these laws in electrical networks lies in their versatility, as they can be applied to a wide range of circuits, from simple series and parallel circuits to more complex electrical networks. Kirchhoff's laws can be employed in conjunction with Ohm's Law, which states that the current through a conductor is proportional to the voltage across it and inversely proportional to its resistance. Using Kirchhoff's and Ohm's Law, engineers can analyze various aspects of a circuit, including voltage drops, current flow, and power distribution.

When analyzing series and parallel circuits, his laws offer valuable insight into the behaviour of electrical components. In series circuits, the current remains constant throughout the entire loop, while the voltage drops across each resistor are proportional to their respective resistances. The voltage across each branch is constant in parallel circuits, but the current is divided among the parallel resistors according to their resistances. By applying KVL and KCL to these configurations, engineers can determine the optimal arrangement of components for a given application.

To illustrate the application of his laws, consider a simple example. Imagine a circuit with a battery, two resistors in series, and a capacitor in parallel with the second resistor. By applying KVL and KCL, we can determine the voltage drop across each resistor, the current flow through each branch, and the voltage across the capacitor, enabling us to analyze the circuit's behaviour under various conditions.

Despite their usefulness, his laws have some limitations and assumptions. For instance, they assume that the components in a circuit are ideal, meaning they have no internal resistance or capacitance. Additionally, they don't account for the effects of electromagnetic fields or the finite speed of signal propagation in AC circuits. However, these limitations are often negligible in many practical applications, as they only marginally impact circuit performance. For a deeper historical context, explore the History of Electricity and the contributions of Gustav Kirchhoff to modern circuit theory.

Related Articles

• Electricity Fundamentals

• Electricity Questions

• Electricity History

Difference Between AC and DC explains alternating current vs direct current, waveform shape, frequency, voltage, polarity, rectification, inversion, power transmission, and typical uses in electronics, grids, batteries, and power supplies.

What Is the Difference Between AC and DC?

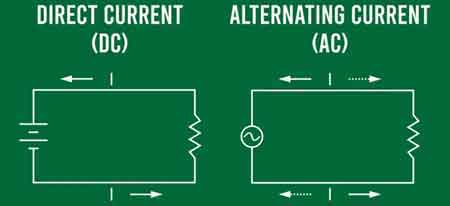
AC reverses direction and frequency; DC is unidirectional. They differ in waveform, voltage, and uses.

✅ AC: sinusoidal waveform; DC: steady line

✅ AC frequency varies by region (50/60 Hz)

✅ Rectifiers convert AC to DC; inverters convert DC to AC

The difference between AC and DC electrical currents is crucial to understand their unique characteristics and diverse applications. By examining the electron flow, voltage variation, power transmission, and safety implications of each current type, we can better appreciate the complex electrical systems that power our daily lives. This comprehensive article offers a deeper understanding of the fundamental distinctions between AC and DC currents, revealing their significance in electricity. For foundational context, see a concise definition of electricity that frames these distinctions clearly.

Two primary types of current dominate the world of electricity: alternating current (AC) and direct current (DC). To understand the difference, we need to explore their unique characteristics, applications, and the principles behind their operation. This comprehensive guide will delve into the details of each electrical current, providing examples and formulas for greater clarity. A broader primer on charge flow is available in this overview of current electricity for readers building fundamentals.

AC (alternating current) and DC (direct current) differ fundamentally in the flow of electrons. In an alternating current, the flow of electrons periodically reverses direction, following a sinusoidal waveform. The waveform is described by the formula V(t) = Vm * sin(2 * π * f * t), where Vm is the maximum voltage, f is the frequency, and t is time. On the other hand, in a direct current, the flow of electrons is constant and unidirectional, resulting in a steady voltage level. For a deeper explanation of sinusoidal behavior, consult this alternating current resource to connect theory with practice.

What is AC electrical current, and how is it measured?

AC (alternating current) is an electrical current in which the flow of electrons periodically reverses direction. Unlike direct current (DC), where the electrons flow in a single, constant direction, alternating current alternates between positive and negative values following a sinusoidal waveform.

AC electrical current is measured in several ways:

Amplitude: The maximum value of the current reached during each cycle is called the amplitude. This is the peak value of the sinusoidal waveform and is typically measured in amperes (A).

RMS (Root Mean Square) value: RMS value is a more practical measurement representing the AC current's effective value. The equivalent DC value would produce the same amount of power as the AC current. To calculate the RMS value of an AC current, you can use the formula I_RMS = I_peak / √2, where I_peak is the peak amplitude of the current.

Frequency: The frequency of an AC current refers to the number of cycles it undergoes per second. It is typically measured in hertz (Hz). In most countries, the standard frequency for AC power systems is either 50 Hz or 60 Hz.

Phase: In AC circuits, multiple currents or voltages may exist with the same frequency but different phase angles. The phase angle is the relative position of the waveform in a complete cycle, measured in degrees (°) or radians. Therefore, it is essential to consider the phase when dealing with multiple AC sources, as it can affect the overall performance of an electrical system.

These measurements are essential for characterizing and analyzing AC electrical currents, allowing engineers and technicians to understand their properties and optimize their use in various applications. For newcomers, this basic electricity primer can reinforce these concepts before moving to advanced analysis.

What is DC electrical current, and how is it measured?

DC (direct current) is a type of electrical current where the flow of electrons is constant and unidirectional. Unlike AC (alternating current), which periodically reverses the direction of electron flow, direct current maintains a consistent flow of electrons from the negative to the positive terminal of a power source. A quick reference on terminology is available in this DC current guide for consistent notation across texts.

DC electrical current is typically measured in a few ways:

Amperes (A): The most common method of measuring DC current is in amperes or amps. An ampere represents the rate of flow of electric charge through a conductor, which remains constant over time in the case of DC. Ammeters or multimeters are typically used to measure DC current in a circuit.

Voltage (V): Voltage is the electrical potential difference between two points in a circuit. For DC circuits, the voltage remains constant over time, providing a stable and predictable power source. The voltage across a power source or components in a DC circuit can be measured using a voltmeter or a multimeter.

Power (W): Power is the rate at which electrical energy is transferred in a circuit. In a DC circuit, power can be calculated using the formula P = V * I, where P is power, V is voltage, and I is current. Power can also be measured directly using specialized equipment like wattmeters.

Resistance (Ω): Resistance is the opposition a conductor offers to the flow of electric current. In a DC circuit, the relationship between voltage, current, and resistance can be described by Ohm's Law, which states V = I * R, where V is voltage, I is current, and R is resistance. Resistance can be measured using an ohmmeter or a multimeter with a resistance measurement function.

These measurements are essential for characterizing and analyzing DC electrical currents, allowing engineers and technicians to understand their properties and optimize their use in various applications, such as batteries, solar panels, and electronic devices. For additional background and historical context, see this direct current explainer covering uses and standards.

Voltage Variation

Voltage variation is an essential aspect that distinguishes AC and DC current. In an AC system, the voltage continuously varies, oscillating between positive and negative values according to the sinusoidal waveform. In contrast, DC voltage remains constant, providing a stable and predictable power source essential for many electrical devices.

Power transmission is another area where AC and DC differ significantly. Alternating current is primarily used for transmitting electricity over long distances due to its ability to utilize transformers. These transformers can adjust the voltage levels, enabling the efficient transmission of electrical energy from power plants to households and businesses. The transmission efficiency is enhanced by reducing current with high voltage and low resistance power lines, which follows the formula P = VI, where P is power, V is voltage, and I is current. On the other hand, direct current is employed in short-range applications. It has gained renewed interest in direct high-voltage current (HVDC) transmission systems for their low losses and efficient long-distance transmission.

Various applications require different electrical current types, making choosing between AC and DC crucial. For example, AC is preferred for most household appliances, such as refrigerators, washing machines, and air conditioners. The power grid provides AC; devices like transformers can easily convert it to the required voltage levels. Conversely, DC is ideal for low-voltage electronics like smartphones, laptops, LED lights, electric vehicles and solar panels that require a stable and consistent power supply. A structured comparison of categories is outlined in this overview of electricity types that helps align choices with applications.

Transformers and converters are key components in AC and DC circuits. In AC systems, transformers use electromagnetic induction to step up or down voltage levels, following the formula Vs/Vp = Ns/Np, where Vs and Vp are the secondary and primary voltages Ns and Np are the number of turns in the secondary and primary coils. In DC systems, converters change voltage levels or convert between AC and DC current power sources using devices like rectifiers and inverters.

Safety implications are paramount when dealing with AC and DC. Both types of electrical current pose potential hazards, including electric shock, burns, and fires. However, AC may be perceived as more dangerous due to its ability to cause muscle contractions, making it difficult to release an electrified object. Regardless, modern safety measures such as grounding, circuit breakers, and fuses have significantly mitigated the risks associated with both types of electrical current.

The unique properties of both currents enable them to serve a wide range of applications, from powering homes and industrial facilities to running delicate electronic devices and renewable energy systems. By grasping the intricacies of voltage, frequency, waveform, conversion, and safety measures, individuals can make informed decisions when choosing between alternating and direct current for specific purposes.

Moreover, the continuing advancements in power transmission technologies, such as direct high-voltage current (HVDC) transmission systems, are bridging the gap between alternating and direct current applications, allowing for more efficient and flexible electricity infrastructure. This progress showcases the importance of understanding both types of electrical currents and their evolving roles in our increasingly interconnected world.

One can explore real-world examples of their use to appreciate the difference between AC and DC further. For example, AC power is harnessed in large-scale power plants, such as coal-fired plants and hydroelectric facilities, which produce electricity using rotating magnets to generate alternating current. In contrast, DC power is often found in batteries, solar panels, and fuel cells, which constantly rely on steady magnetism or chemical reactions to flow electrons.

Related Articles

• Electricity Fundamentals

• Electricity Questions

• Electricity History

Total impedance calculator determines total opposition in AC circuits by combining resistance, inductive reactance, and capacitive reactance. Input R, L, C, and frequency to find Z in ohms for accurate analysis in power distribution, filters, or signal systems.

Quick Definition: Total Impedance Calculator

• ✅ Purpose: Calculates total opposition (impedance) in AC circuits by combining resistance and reactance.

• ✅ Functionality: Processes inputs like resistance (R), inductance (L), capacitance (C), and frequency to compute impedance (Z).​

• ✅ Applications: Used in designing power supplies, signal transmission systems, and optimizing filter performance.​

A total impedance calculator helps you quickly determine the combined impedance of resistors, inductors, and capacitors in AC circuits. By inputting values for resistance (R), inductive reactance (XL), and capacitive reactance (XC), you can calculate total impedance (Z) for both series and parallel configurations, making circuit analysis faster, more accurate, and easier to understand. A total impedance calculator is a powerful tool used by electrical engineers, technicians, and students to determine the impedance in RLC circuits, whether in series or parallel. These calculators simplify complex calculations involving resistance, inductance, and capacitance by processing formulas that would otherwise require manual computation with complex numbers.

Whether you are designing a power supply, analyzing signal transmission, or optimizing filter performance, a total impedance calculator helps ensure accuracy and efficiency. It is especially valuable when analyzing the behaviour of AC circuits across different frequency ranges in hertz.

What Is Total Impedance?

Total impedance refers to the combined opposition that a circuit presents to the flow of alternating current. It takes into account both resistance (R) and reactance (X), expressed as a single value in ohm (Ω). The two primary types of reactance are:

• Inductive reactance (caused by coils or inductors)

• Capacitive reactance (caused by capacitors)

These values change depending on the circuit's frequency, making tools like a total impedance calculator essential for real-time circuit analysis.

Who Uses a Total Impedance Calculator?

• Electrical engineers use it in power systems, communications, and control circuits.

• Technicians rely on it to verify component ratings and troubleshoot systems.

• Educators and students apply it in academic settings for lab work and theoretical analysis.

• Industrial maintenance professionals use it to evaluate equipment behavior under various loads.

It is particularly helpful when working with an RLC circuit impedance calculation where both inductance (L) and capacitance (C) are present.

What Does a Total Impedance Calculator Do?

A good impedance calculator lets you:

• Enter known values like resistance (R), inductance L and capacitance C, and frequency in hertz.

• Automatically compute impedance for either series RLC circuit or parallel RLC circuit setups.

• Show results using the correct impedance formula, including both magnitude and phase.

• Factor in angular frequency in rad, derived from ω=2πf\omega = 2\pi fω=2πf, where fff is frequency.

• Solve expressions like 1ωC\frac{1}{\omega C}ωC1​ or frac 1 omega, commonly used in capacitive reactance calculations.

The result is a fast, accurate way to determine the impedance and analyze AC circuit behavior.

Key Concepts Behind the Calculator

1. Impedance Formula (Z)

This requires working with complex numbers to calculate both magnitude and phase angle.

2. Reactance Components

• Inductor and capacitor components contribute to the reactive part of the impedance.

• Capacitive reactance

• Inductive reactance

These values vary with frequency and affect circuit resonance and behavior.

Why Use a Total Impedance Calculator?

Without a calculator, these formulas can be tedious to evaluate manually—especially when working in real time or across wide frequency in hertz ranges. A calculator ensures:

• Greater accuracy in design and testing

• Time-saving analysis for troubleshooting

• Safer decision-making for load balancing and component selection

In power electronics, knowing the rlc circuit impedance helps prevent equipment damage and improves system efficiency.

A total impedance calculator is an essential tool for modern electrical work. It brings together the core principles of AC circuit analysis—resistance, inductance, capacitance, and frequency—into one user-friendly interface. Whether you're designing systems, teaching students, or maintaining equipment, using this tool helps you quickly and reliably calculate the impedance and make informed decisions.

Related Articles

• Apparent Power Formula

• Resistive Load Types

• Lagging Power Factor

• Power Quality Overview

Electricity generation is the process of producing electric power from various energy sources, including fossil fuels, solar, wind, hydro, and nuclear. It uses turbines and generators to convert mechanical or thermal energy into electrical energy for residential, commercial, and industrial use.

What is Electricity Generation?

Electricity generation is a process that involves producing electrical power from various sources.

✅ Converts mechanical, thermal, or chemical energy into electrical power

✅ Uses generators powered by steam, wind, water, or combustion

✅ Essential for powering homes, industries, and transportation

In the United States, power production from utility-scale generators was about 4.1 trillion kilowatt-hours (kWh) in 2019. Fossil fuels, including coal, natural gas, and petroleum, produced about 63% of the electricity, while nuclear energy produced around 20%. The remaining 17% was generated from renewable energy sources, including solar photovoltaics, wind turbines, and hydroelectric power production. To explore the full process from fuel to flow, see our detailed guide on how electricity is generated.

Electricity Generation Sources Compared

Hydroelectric Power Generation

Hydroelectric power production units utilize flowing water to spin a turbine connected to a generator. Falling water systems accumulate water in reservoirs created by dams, which then release it through conduits to apply pressure against the turbine blades, driving the generator. In a run-of-the-river system, the force of the river current applies pressure to the turbine blades to produce power. In 2000, hydroelectric generation accounted for the fourth-largest share (7 percent) of electricity production, at 273 billion kWh. Explore how water and electricity interact in hydroelectric plants, where falling water is converted into renewable energy.

Non-Hydro Renewable Energy Sources in Electricity Generation

Non-water renewable sources, including geothermal, refuse, waste heat, waste steam, solar thermal power plants, wind, and wood, contribute only small amounts (about 2 percent) to total power production. In 2019, power production from these sources totalled 84 billion kWh. The entire electric power industry production in 2019 was 3,800 billion kWh, with utilities' net production accounting for 3,015 billion kWh and net generation by non-utility power producers 785 billion kWh.

U.S. Electricity Generation by Energy Source: Trends and Shifts

The United States' share of electrical energy production from different sources has changed more rapidly since 2007 than ever since 1950. On the other hand, Canada's energy production is significantly less than that of the USA, primarily in Ontario and British Columbia. At least three trends are catalyzing these changes: (1) the low price of natural gas; (2) the rise in renewable and distributed generation due to falling costs; and (3) recent Federal and State policies impacting production. There are many innovative ways to generate electricity, from traditional fossil fuels to cutting-edge renewable technologies.

Fuel Source Diversity in U.S. and Canadian Electricity Production

Diversity is a key attribute in U.S. and Canadian electricity production. However, rather than being the result of a deliberative, long-term national initiative, this diversity has developed through spurts of growth in specific production technologies at different times. This is often due to policies, historical events, capital costs, fuel costs, and technological advancements.

Historical Growth of Electricity Generation by Energy Source

Most energy sources have experienced eras of significant capacity growth in terms of terawatt hours: hydro (1930‒1950, not shown); coal (1950-1985); nuclear (1960‒1980); natural gas (1990‒2010); and renewables (2005‒present). Nuclear energy is increasingly recognized as a key solution for achieving carbon reduction goals—learn how it contributes to net-zero emissions.

Changing U.S. Power Generation Mix: Centralized to Distributed Energy

The U.S. generation mix has undergone significant changes over the past few decades and is projected to continue evolving substantially. The U.S. generation fleet is transitioning from one dominated by centralized generators with high inertia and dispatchability to one more hybridized, relying on a mixture of traditional, centralized production and variable utility-scale and distributed renewable energy production.

Power Generation Technologies: From Diesel Engines to Wind Turbines

To generate power, various sources are utilized, including diesel engines, gas turbines, and nuclear power plants. Fossil fuels, including natural gas and coal, are burned to create hot gases that go through turbines, which spin the copper armature inside the generator and generate an electric current. In a nuclear power plant, nuclear reactions generate heat that is used to heat water, which then turns into steam and passes through a turbine to produce electricity. In a wind turbine, the wind pushes against the turbine blades, causing the rotor to spin and generating an electric current. In a hydroelectric turbine, flowing or falling water pushes against the turbine blades, causing the rotor to spin and generating an electric current. As the global energy landscape evolves, many experts are re-evaluating the role of nuclear power—learn more in our feature on the future of nuclear energy.

Electricity Generation by Utilities and Non-Utility Power Producers

To meet these immediate demands, utilities and nonutility power producers operate several electric generating units powered by various fuel sources. Renewable fuels, such as water, geothermal, wind, and other renewable energy sources like solar photovoltaics, are used as sources of power, alongside fossil fuels and uranium.

Fossil Fuel Electricity Generation: Coal, Natural Gas, and Petroleum

Coal was the fuel used to generate the largest share (51.8 percent) of electricity in 2000, with natural gas and petroleum accounting for 16.1 percent and 3 percent, respectively. Steam-electric generating units burn fossil fuels, such as coal, natural gas, and petroleum, to produce steam. This steam is then used to turn a turbine into a generator, producing power. On the other hand, gas turbine generators burn fuels to create hot gases, which also go through a turbine, spinning the copper armature inside the generator and generating an electric current. Diesel engine generators are also used, where the combustion occurs inside the engine's cylinders, which are connected to the generator's shaft. The mechanical energy provided by the turbine drives the generator, which in turn produces energy.

Electricity Generation Trends and the Global Shift Toward Renewables

The production of electrical energy has experienced various eras of significant capacity growth in the United States, Canada, and other countries worldwide. The future of power production is transitioning to a more hybridized generation fleet that relies on a combination of traditional, centralized power production and variable utility-scale and distributed renewable energy sources. Low natural gas prices drive this transition, the rise of renewable and distributed energy sources, and recent Federal and State policies that impact generation. Discover the most common renewable energy sources powering the shift toward a cleaner, more sustainable electricity future.

Enhance your expertise in clean energy with our comprehensive Renewable Energy Grid Integration Training course. Designed for electrical professionals, this course covers the challenges and solutions associated with connecting solar, wind, and other renewable energy sources to the power grid. Stay ahead of industry trends, improve system reliability, and gain valuable skills to support the transition to a sustainable energy future. Enroll today and take the next step in your professional development.

Frequently Asked Questions

How is electricity generated from renewable energy sources?

Electricity is generated from renewable energy sources by converting the energy of the sun, wind, water, or earth into electrical energy. For example, solar photovoltaic panels generate power directly from sunlight, wind turbines to generate electricity from wind energy, and hydroelectric power plants generate power from falling water.

What are the different types of fossil fuels used?

The different types of fossil fuels used include coal, natural gas, and petroleum. Coal is the most commonly used fossil fuel for energy production, followed by natural gas and oil.

What are the advantages and disadvantages of using nuclear power plants for electricity generation?

Advantages of using nuclear power plants include that they produce a large amount of energy with a low amount of fuel, emit less carbon dioxide than fossil fuel power plants, and are not dependent on weather conditions like wind or solar power. Disadvantages include the risks associated with nuclear accidents, the high cost of building and maintaining nuclear power plants, and the long-term storage of nuclear waste.

How do gas turbines work to generate electricity?

Gas turbines burn natural gas or other fuels to heat air, which expands and drives the turbine. Finally, the turbine is connected to a generator that converts the mechanical energy of the turbine into electrical energy.

What is the role of steam turbines in electricity generation?

Steam turbines are commonly used to convert thermal energy from steam into mechanical energy that drives a generator. Steam is produced by burning fossil fuels or using heat from nuclear reactions or geothermal sources. The steam drives the turbine blades, which are connected to the generator to produce electricity.

What are some examples of non-renewable energy sources?

Examples of non-renewable energy sources used for power production include fossil fuels, such as coal, natural gas, and petroleum, as well as nuclear energy.

How is electricity generated and distributed in the United States?

Various power plants, including those powered by fossil fuels, nuclear energy, and renewable energy sources, generate electricity in the United States. Electric power is transported over a complex network of power lines and transformers to homes, businesses, and other consumers through local utility companies. The Federal Energy Regulatory Commission (FERC) and various state regulatory agencies regulate power distribution.

Related Articles

• Renewable Energy Channel

• Energy Storage Channel

• Electricity Forum