Capacitance Explained

Capacitance: Understanding the Ability to Store Electricity

Capacitance is an essential concept in electrical circuits, and it describes the ability of a capacitor to store electrical energy. Capacitors are electronic components used in many circuits to perform various functions, such as filtering, timing, and power conversion. Capacitance is a measure of a capacitor's ability to store electrical energy, and it plays a crucial role in the design and operation of electrical circuits. This article provides an overview of capacitance, including its definition, SI unit, and the difference between capacitor and capacitance.

What is Capacitance?

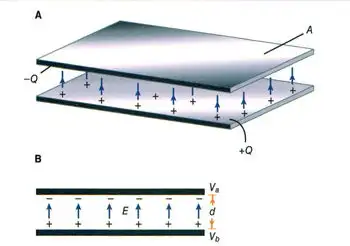
Capacitance is the ability of a capacitor to store electrical charge. A capacitor consists of two conductive plates separated by a dielectric material. The conductive plates are connected to an electrical circuit, and the dielectric material is placed between them to prevent direct contact. When a voltage source is applied to the plates, electrical charge builds up on the surface of the plates. The amount of charge that a capacitor can store is determined by its capacitance, which depends on the size and distance between the plates, as well as the dielectric constant of the material.

The energy storing capability of a capacitor is based on its capacitance. This means that a capacitor with a higher capacitance can store more energy than a capacitor with a lower capacitance. The energy stored in a capacitor is given by the formula:

Energy (Joules) = 0.5 x Capacitance (Farads) x Voltage^2

The ability to store energy is essential for many applications, including filtering, timing, and power conversion. Capacitors are commonly used in DC circuits to smooth out voltage fluctuations and prevent noise. They are also used in AC circuits to filter out high-frequency signals.

What is Capacitance and the SI Unit of Capacitance?

Capacitance is defined as the ratio of the electrical charge stored on a capacitor to the voltage applied to it. The SI unit of capacitance is the Farad (F), which is defined as the amount of capacitance that stores one coulomb of electrical charge when a voltage of one volt is applied. One Farad is a relatively large unit of capacitance, and most capacitors have values that are much smaller. Therefore, capacitors are often measured in microfarads (µF) or picofarads (pF).

The capacitance of a capacitor depends on several factors, including the distance between the plates, the surface area of the plates, and the dielectric constant of the material between the plates. The dielectric constant is a measure of the ability of the material to store electrical energy, and it affects the capacitance of the capacitor. The higher the dielectric constant of the material, the higher the capacitance of the capacitor.

What is the Difference Between Capacitor and Capacitance?

Capacitor and capacitance are related concepts but are not the same thing. Capacitance is the ability of a capacitor to store electrical energy, while a capacitor is an electronic component that stores electrical charge. A capacitor consists of two conductive plates separated by a dielectric material, and it is designed to store electrical charge. Capacitance is a property of a capacitor, and it determines the amount of electrical charge that the capacitor can store. Capacitance is measured in Farads, while the capacitor is measured in units of capacitance, such as microfarads (µF) or picofarads (pF).

What is an Example of Capacitance?

One example of capacitance is a common electronic component known as an electrolytic capacitor. These capacitors are used in a wide range of electronic circuits to store electrical energy, filter out noise, and regulate voltage. They consist of two conductive plates separated by a dielectric material, which is usually an electrolyte. The electrolyte allows for a high capacitance, which means that these capacitors can store a large amount of electrical energy.

Another example of capacitance is the human body. Although the capacitance of the human body is relatively small, it can still store a significant amount of electrical charge. This is why people can sometimes feel a shock when they touch a grounded object, such as a metal doorknob or a handrail. The capacitance of the human body is affected by several factors, including the size and shape of the body, as well as the material and proximity of the objects it comes into contact with.

Related News

Water Electricity

Water electricity refers to electrical power generated using water, primarily through hydroelectric systems. It converts the kinetic energy of moving or falling water into electricity, providing a renewable and sustainable energy source with low carbon emissions and high efficiency.

What is: “Water Electricity?”

Water electricity, also known as hydroelectric power, is energy derived from moving water. It’s a leading source of renewable electricity worldwide.

✅ Converts water’s kinetic energy into usable electricity

✅ Offers renewable, low-emission electricity generation

✅ Used in dams, rivers, and tidal energy systems

Most hydroelectric power is generated from the potential energy of dammed water, which drives a water turbine and generator. Less common variations utilize water's kinetic energy or undammed sources, such as tidal power. Hydroelectricity is a renewable energy source.

The energy extracted from water depends not only on the volume but on the difference in height between the source and the water's outflow. This height difference is referred to as the head. The amount of potential energy in water is directly proportional to the head. To obtain a very high head of water for a hydraulic turbine, water may be run through a large pipe called a penstock.

While many supply public power networks, some Water Electricity projects were created for private commercial purposes. For example, aluminum processing requires substantial amounts of power, and in Britain's Scottish Highlands, there are examples at Kinlochleven and Lochaber, designed and constructed during the early 20th century. Similarly, the 'van Blommestein' lake, dam and power station were constructed in Suriname to provide power for the Alcoa aluminum industry. In many parts of Canada (specifically, the provinces of British Columbia, Manitoba, Ontario, Quebec, and Newfoundland and Labrador), hydroelectricity is used so extensively that the word "hydro" is often used to refer to any power delivered by a power utility. The government-run power utilities in these provinces are called BC Hydro, Manitoba Hydro, Hydro One (formerly "Ontario Hydro"), Hydro-Québec and Newfoundland and Labrador Hydro, respectively. Hydro-Québec is the world's largest hydroelectric generating company, with a total installed capacity (2005) of 31,512 MW. For deeper insight into how to generate electricity from various sources, including water, visit our guide on hydroelectricity, which explains methods, systems, and real-world examples.

Importance

Water and Electricity power supplies 20% of the world's electricity. Norway produces virtually all of its energy from hydroelectric sources. In contrast, Iceland produces 83% of its requirements (as of 2004), and Austria generates 67% of all power in the country from hydroelectric sources (over 70% of its total requirements). Canada is the world's largest producer of Water Electricity, and produces over 70% of its electric power from hydroelectric sources.

Apart from a few countries with an abundance of it, hydro capacity is normally applied to peak-load demand, because it can be readily stored during off-peak hours (in fact, pumped-storage hydroelectric reservoirs are sometimes used to store power produced by thermal plants for use during peak hours). It is not a major option for the future in developed countries because most major sites in these countries that have the potential for harnessing gravity in this way are either already being exploited or are unavailable for other reasons, such as environmental considerations.

Regions where thermal plants provide the dominant supply of power utilize Water Electricity to provide the important functions of load following and regulation. This permits thermal plants to be operated closer to thermodynamically optimal points rather than varied continuously, which reduces efficiency and potentially increases pollutant emissions. Concurrently, hydro plants are then utilized to provide for hour-to-hour adjustments and to respond to changes in system frequency and voltage (regulation), with no additional economic or environmental effect.

Electricity Prices Explained

Electricity prices reflect tariffs, kWh rates, time-of-use schedules, peak demand charges, and grid congestion, driven by generation costs, transmission losses, and load profiles in power systems and industrial electrical engineering.

What Are Electricity Prices?

Electricity prices are costs per kWh shaped by tariffs, time-of-use, demand charges, and grid operating constraints.

✅ Defined per kWh with time-of-use and demand charges

✅ Influenced by generation mix, transmission losses, congestion

✅ Managed via load control, demand response, smart metering

Electricity prices, or rates, are usually determined by electric utilities and the governmental organizations that oversee them. The fees an electric utility company charges its customers for service aer based on electricity prices set by government, except in the case where they cost electricity prices on a deregulated basis. In that case, electricity prices are determined by marketplace factors such as supply and demand. Electric utility companies charge their customers different rates, depending on the type of customer, the kind of contract, and on the customer's needs. Electricity Prices bill energy on the kwh basis of the individual customer's rate, the level of consumption, and other charges, such as taxes and fuel adjustments. This is how electricity billed. For a deeper breakdown of typical rate components, resources like electricity cost guides explain line items and surcharges clearly.

That collection of rates is called a tariff. The power tariff is designed to provide the privately owned electric utility with enough income to allow investors to earn a cash return and cover operation and maintenance costs. Most of the larger utilities operate as regulated franchises, meaning that the prices they charge are subject to public review, often by a State public utility commission. In competitive markets, customers may choose an electricity supplier while the utility still handles delivery services and billing oversight.

Publicly owned electric utilities are nonprofit, local government agencies established to provide service to their communities and nearby consumers at cost, returning excess funds to the consumer in the form of community contributions, more economic and efficient facilities, and lower power rates. To meet these community objectives, public power agencies plan their electricity supply over multiyear horizons to manage risk and affordability.

Publicly owned electric utilities (which number approximately 2,000) include municipals, public power districts, State authorities, irrigation districts, and other State organizations. Some of these organizations also own or contract for electricity generation assets to enhance self-sufficiency and rate stability.

There are approximately 900 cooperative electric utilities in the United States currently doing business in 47 States. These utilities are owned by their members and are established to provide power to those members. Because member education supports better usage decisions, many cooperatives provide primers on what electricity is and how it is measured on bills.

Average retail Electricity prices of power are calculated by dividing utility revenue by retail sales. The resulting measurement is the cost, or average revenue per kilowatthour, of power sold. (A kilowatthour is equal to one watt of power supplied to an electric circuit steadily for 1,000 hours.) Electric utilities usually offer three primary classes of service: residential, commercial, and industrial. The average price per kilowatthour for residential consumers is generally higher than for any other sector due in part to higher costs associated with serving many consumers who use relatively small amounts of power. In Ontario, the industrial sector has the lowest energy prices and energy bills rates every month due to the economies of serving a few consumers who use relatively large amounts of electricity. Understanding the distinction between energy in kilowatthours and instantaneous electricity power demand helps customers interpret peak charges and capacity fees. Regional consumption patterns, including trends in electricity demand in Canada, can influence wholesale prices and cross-border power flows affecting local rates.

average retail

Sources of Electricity Explained

Sources of electricity include fossil fuels, nuclear power, and renewable energy like solar, wind, and hydro. These energy sources provide reliable electricity generation, powering homes, industries, and grids while shaping modern energy systems and sustainability goals.

What are the Sources of Electricity?

Sources of electricity are the various energy systems used to generate electrical power, ranging from conventional fuels to renewable technologies.

✅ Include fossil fuels, nuclear power, and renewable energy

✅ Used in electricity generation across all sectors

✅ Impact cost, sustainability, and environmental footprint

In the modern world, electricity plays a crucial role in our daily lives. As a result, it has become an essential commodity, from powering our homes to running industries. But have you ever wondered where it comes from? Electric power can be generated from various sources with unique characteristics, benefits, and drawbacks. In this article, we'll delve into the main sources of electric power generation and discuss their environmental impacts, costs, and efficiency. Renewable sources, such as hydro, solar, and wind, contrast with alternative electricity options that aim to reduce dependence on fossil fuels.

The primary sources of electric power used to produce electric power can be broadly categorized into renewable and non-renewable resources. Renewable energy sources, such as solar, wind, hydroelectric, geothermal, and biomass, are replenished naturally and have a lower environmental impact than non-renewable sources. Non-renewable energy sources include fossil fuels such as coal, natural gas, and oil, as well as nuclear energy. These resources are finite, and their extraction and utilization contribute to environmental issues like air pollution and climate change. Hydroelectric dams, wind turbines, and solar farms all contribute to global electricity generation, reducing reliance on non-renewable sources.

According to the U.S. Energy Information Administration, global electricity production relies on a mix of renewable and non-renewable sources. While traditional thermal power plants, fueled by coal, natural gas, and nuclear energy, remain central to electricity generation, the rapid growth of solar photovoltaics is transforming how we create and consume electricity. Many nations are investing heavily in utility-scale electricity projects, from massive solar farms to offshore wind facilities, to meet rising demand while reducing emissions. These shifts illustrate how diverse technologies collectively shape the future of reliable and sustainable power.

Fossil Fuels: The Traditional Backbone

Fossil fuels remain the dominant source of electricity worldwide. In 2023, they accounted for roughly 61% of global power generation. In the U.S., about 60% of electric power still comes from coal, natural gas, and oil. These fuels are burned to produce heat, which converts water into steam that drives turbines to generate electric power.

While fossil fuels offer reliability and established infrastructure, they release large amounts of greenhouse gases, contributing significantly to air pollution and climate change.

Nuclear Energy: Low Carbon but Controversial

Nuclear energy provides approximately 9% of the world's electric power and nearly 19% in the United States. It works by splitting atoms (nuclear fission) to release energy that turns water into steam, which then drives turbines.

Nuclear power is highly efficient and emits no carbon during operation. However, it poses concerns regarding radioactive waste, high capital costs, and the potential for catastrophic failures.

Renewable Energy: The Fastest-Growing Sector

Renewable energy sources are expanding rapidly due to technological advances and falling costs. In 2023, they accounted for approximately 30% of global electric power, with wind and solar energy experiencing the fastest growth. Among renewables, Geothermal Electricity harnesses Earth’s internal heat to produce reliable baseload power even in regions with limited solar or wind potential.

Solar Power

Solar energy converts sunlight into electric power using photovoltaic cells, also known as photovoltaic panels. It's scalable, from rooftop systems to massive solar farms, and has seen significant cost reductions over the past decade.

Wind Power

Wind turbines capture kinetic energy from the wind to generate electric power. Wind farms are increasingly common in the U.S., Europe, and China. Like solar energy, wind energy is intermittent, but storage technology is continually improving.

Hydroelectric Power

Hydroelectricity uses flowing water to turn turbines. It's the most established renewable source and provides reliable base-load power. However, large dams can disrupt ecosystems and displace communities. Hydroelectricity stands out as a mature and stable form of renewable generation, as detailed on our Hydroelectricity page.

Geothermal and Biomass

Geothermal taps into Earth’s internal heat, while biomass burns organic material. While smaller in scale, both contribute to energy diversity and localized solutions. Geothermal power generation complements solar, wind, and hydroelectric sources by offering a steady, round-the-clock output, as explained in our detailed guide on Geothermal Electricity.

Comparing Sources of Electricity

Source	Global Share (2023)	U.S. Share (2023)	Key Advantages	Key Drawbacks
Fossil Fuels	~61%	~60%	Reliable, established infrastructure	High emissions, non-renewable
Nuclear	~9%	~19%	Low carbon, high efficiency	Radioactive waste, high cost
Renewables	~30%	~21%	Clean, sustainable, fast-growing	Intermittent, resource/location dependent

The diverse world of electric power choices offers a range of technologies that can help meet the growing global demand for energy. By understanding the characteristics, environmental impacts, costs, and efficiencies of these sources, we can make informed decisions about transitioning to cleaner, more sustainable energy systems. As renewable energy technologies continue to advance and energy storage solutions mature, the future of electric power generation is likely to be increasingly dominated by clean, sustainable sources that reduce our impact on the planet and provide reliable power for future generations.

Environmental Impact and Efficiency

The environmental effects of each source vary significantly:

Coal and oil are the dirtiest, producing the most CO2 and pollutants.
Natural gas emits less CO2 but still contributes to climate change.
Nuclear has a low operational footprint but long-term waste issues.
Solar and wind energy produce no emissions during use, although manufacturing has some environmental impact.

Efficiency also differs:

Natural gas plants can achieve thermal efficiencies exceeding 60%.
Nuclear reactors are highly efficient, but they are slow to build.
Coal is among the least efficient.
Renewables vary based on technology and location.

Cost Considerations

Costs are influenced by technology, fuel, geography, and infrastructure:

Solar and wind costs have dropped dramatically, making them competitive with fossil fuels.
Nuclear has high upfront costs but low operating costs.
Fossil fuels fluctuate in response to changes in market supply and demand.

Future Trends in Power Generation

The energy sector is moving toward decarbonization. Key trends include:

Growth in solar and wind capacity
Advances in energy storage systems
Development of smart grids and microgrids
Investment in fusion energy research

Many countries are setting net-zero goals, aiming for cleaner and more sustainable electricity systems.

Electric power can be generated from various sources, each with its trade-offs in terms of cost, efficiency, and environmental impact. While fossil fuels still dominate, the momentum is clearly shifting toward renewable energy sources. A diversified energy mix, supported by smart technologies and forward-looking policies, will power the sustainable future. To understand how energy sources are converted into power, refer to our 'Generate Electricity' article, which describes the entire process from fuel or resource to grid delivery.

Understanding the strengths and weaknesses of each source helps shape a more resilient, efficient, and eco-friendly power generation landscape. Whether from fossil fuels, nuclear, or renewables, every source of electricity must connect to the electricity grid to deliver power where it is needed.

Electricity Supply And Demand Balance

Electricity supply covers generation, transmission, distribution, grid infrastructure, voltage regulation, frequency control, power quality, protection, SCADA, and load management to ensure reliable energy delivery to industrial, commercial, and residential loads.

What Is Electricity Supply?

Electricity supply is generation, transmission and distribution of power with set voltage, frequency and reliability.

✅ Involves generation, HV transmission, MV/LV distribution networks

✅ Ensures voltage regulation, frequency control, and power quality

✅ Uses SCADA, protection relays, and load forecasting for reliability

What Is Electricity Supply?

Electricity Supply is a complex balanced system of electric power generation and real time customer demand. Production (supply) and consumption (demand) dictate electricity pricing in the United States and Canada. For a regional view, the analysis at Electricity Demand in Canada highlights how seasonal peaks and resource availability shape prices.

Where does the term "electricity supply" originate? How does that supply move from one point to another? These are most important questions to ask when you want to understand the electric power industry.

If you're new to the vocabulary, the concise glossary at Electricity Terms can clarify definitions used throughout the industry.

The first thing to know is that electric power is generated in the United States and Canada in power plants which house electrical generators. Then, power is transported (transmission and distriubtution) through the power grid to the customer. This complex network of transmission lines delivers power to industrial, commercial, institutional and residential customers. For a step-by-step overview of system operations, Electricity: How It Works explains generation, transmission, and distribution in practical detail.

In the electricity industry, transmission and distribution wires do the work of transporting power to satisfy electricity demand during real time peak demand. This is the job of the electricity market. The natural gas and fossil fuels industry works in the same way. These lines run from generating station to substations (sometimes over great distances, like in the case of British Columbia and Manitoba where generation is in the far north and the consumption is in the south. This is where the voltage is reduced for local consumption. Substations are usually located close to where the electricity is consumed.

For background on core power concepts, the primer at Electricity Power connects voltage, current, and load to real-world grid behavior.

The various prices of electricity depends on the electricity supply mix and the energy efficiency of the customer. Electricity energy supply is usually measured in terawatt hours.

The system design is of three-phase alternating current electrical generation and distribution, which was invented by Nikola Tesla in the 19th century. He considered that 60 Hz was the best frequency for alternating current (AC) power generating Electricity Supply. He preferred 240 V, which was claimed to be better for long supply lines. Thomas Edison developed direct current (DC) systems at 110 V and this was claimed to be safer. For more information about the early battles between proponents of AC and DC supply systems see War of Currents. For foundational fundamentals beyond this history, the overview at What Is Electricity clarifies the principles common to both AC and DC systems.

The German company AEG built the first European generating facility to run at 50 Hz, allegedly because the number 60 did not fit into the numerical unit sequence of 1, 2, 5…. At that time, AEG had a virtual monopoly and their standard spread to the rest of the continent. In Britain, differing frequencies (including 25 Hz 40 Hz and DC) proliferated, and the 50 Hz standard was established only after World War II.

To see how frequency standards interact with generation and end-use performance, the explainer at How Electricity Works ties design choices to everyday operation.

Originally much of Europe was 110 V too, just like the Japanese and the US system today. It was deemed necessary to increase the necessary voltage to draw more electrical power with reduced energy loss and voltage drop from the same copper wire diameter.

The choice of utilization voltage is governed more by tradition than by optimization of the distribution system. In theory, a 240 V distribution system will use less conductor material to deliver a given quantity of power. Incandescent lamps for 120 V systems are more efficient and rugged than 240 V lamps, while large heating appliances can use smaller conductors at 240 V for the same output rating. Practically speaking, few household appliances use anything like the full capacity of the outlet to which they are connected. Minimum wire sizes for hand-held or portable equipment is usually restricted by the mechanical strength of the conductors. One may observe that both 240 V system countries and 120 V system countries have extensive penetration of electrical appliances in homes. National electrical codes prescribe wiring methods intended to minimize the risk of electric shock or fire. For household applications, home electricity basics show how these voltage considerations affect outlets, circuits, and safety practices.

Areas using (approximately) 120V allow different combinations of voltage, suitable for use by a variety of classes of electrical equipment.

Watthour Meter Explained

A watthour meter measures electrical energy consumption in kilowatt-hours (kWh) for residential, commercial, and industrial applications, ensuring accurate billing, energy management, and compliance with utility standards.

What is a Watthour Meter?

✅ Measures total electrical energy in kilowatt-hours (kWh) over time

✅ Supports accurate billing, energy monitoring, and demand analysis

✅ Used in residential, commercial, and industrial revenue metering

Advancements in Watthour Meter Technology and Energy Measurement

Watthour meter technology plays a crucial role in modern electrical engineering and maintenance by providing accurate measurement and monitoring of energy consumption. These devices are indispensable for managing energy efficiency, optimizing power distribution, and ensuring compliance with regulatory standards. For electrical professionals, understanding how they operate and are maintained is essential to minimize energy losses and enhance the reliability of electrical systems. With the growing demand for precise energy data in both residential and industrial applications, staying informed about advancements in watthour meter technology is more important than ever. Understanding how a watthour is calculated helps clarify how a watthour meter tracks total energy usage for accurate billing.

How Induction Type Single Phase Watt Hour Meters Work

Induction type meters, commonly used as single phase watt hour meters, provide accurate measurement of electrical energy consumption in residential and small commercial installations.

Your electric utility is not too interested in how much power you're consuming for one appliance or even how much power a single household is drawing at any given time. By far the greater concern is the total energy that is used over a day, a week, a month or a year. Electrical energy is measured in watt-hours or, more commonly for utility purposes, in kilowatt-hours (kWh). The device that measures this consumption is the watt-hour meter or kilowatt-hour meter. For a deeper understanding of the units used in metering, see our guide on electrical energy and how it is measured in kilowatt-hours.

The most common method for measuring electrical energy is by using a small electric motor device, whose speed depends on the current, and thereby on the power at a constant voltage. The number of turns of the motor shaft, in a given length of time, is directly proportional to the number of watt hours consumed. The motor is placed at the point where the utility wires enter the house, apartment or building. This is usually at a point where the voltage is 234 V. This is split into some circuits with 234 V, for heavy-duty appliances such as the oven, washer and dryer, and the general household circuits for lamps, clock radios and television sets. The principles behind watthour meters are closely tied to basic electricity and the relationship between active power and time.

Understanding the Spinning Disk in Electromechanical Watthour Meters

You've surely seen the little disk in the utility meter going around and around, sometimes fast, other times slowly. Its speed depends on the power you're using. The total number of turns of this little disk, every month, determines the size of the bill you will get, as a function also, of course, of the cost per kilowatt hour for electricity.

Kilo-watt-hour meters count the number of disk turns by means of geared, rotary drums or pointers. The drum-type meter gives a direct digital readout. The pointer type has several scales calibrated from 0 to 9 in circles, some going clockwise and others going counterclockwise. Mechanical and electronic meters both rely on the concepts of electrical resistance and current to provide precise readings.

How to Read a Pointer-Type Watthour Meter Accurately

Reading a pointer-type utility meter is a little tricky because you must think in whatever direction (clockwise or counterclockwise) the scale goes. An example of a pointer-type utility meter is shown in Fig. 3-11. Read from left to right. For each little meter, take down the number that the pointer has most recently passed. Write down the rest as you go. The meter in the figure reads 3875 kWh. If you want to be really precise, you can say it reads 3875-1/2 kWh. To place watt hour metering in historical context, explore our history of electricity page and learn how early meters evolved into today’s advanced devices.

Fig. 3-11 An example of a utility kilo-watthour meter. The reading is a little more than 3875 kWh.

Electricity Supplier - Make The Right Choice

Electricity supplier delivers power via transmission and distribution networks, managing tariffs, load forecasting, SCADA, and power quality, integrating renewables, smart meters, and demand response to ensure grid reliability, compliance, and efficient kWh billing.

What Is an Electricity Supplier?

An electricity supplier procures and delivers power, manages tariffs, and ensures grid reliability and power quality.

✅ Energy procurement and wholesale market participation

✅ Distribution coordination, SCADA monitoring, and outage management

✅ Tariff design, metering, billing, and power quality compliance

Who is my electricity supplier?

In Canada and the United States, it’s easy to learn which energy provider serves your property or residence. It depends on whether you are trying to find your electricity and natural gas supplier. Sometimes, homes and businesses have the power to choose their energy service utility company and the products and service they provide. Customers are free to choose. It's a competitive energy marketplace. For a plain-language primer on infrastructure, see the electricity supply overview to understand typical delivery steps.

If you use both services, your property might have the same local distribution company for both fuels, – commonly known as a "duel fuel supplier". But if your utility records are stored separately, you might need to more research to learn who supplies your natural gas services and your electricity services separately. If you are curious where the power originates, this guide to how electricity is generated explains common fuel sources and grid integration.

Here is a list of accredited Electricity Suppliers in Canada

https://www.ic.gc.ca/eic/site/mc-mc.nsf/eng/lm00525.html

Market dynamics can vary by province, and recent electricity demand trends in Canada help explain seasonal shifts in offers.

Here is a list of accredited Electricity Suppliers in the United States.

https://www.electricchoice.com/blog/25-top-providers-part-1/

When comparing providers, consult current electricity price benchmarks to contextualize quoted rates.

Who can supply electricity?

All electricity supplier companies must have a licence from the Office of Gas and Electricity Markets (Ofgem). One of the licence conditions is that a company must produce codes of practice on:

Although the codes of practice are not legally enforceable, they will be useful when negotiating with a company and any breach should be reported to governmental regulatory authorities. Understanding the basics in this introduction to what electricity is can make those obligations clearer.

Choosing an electricity supplier

You can change your company if you wish. If you are considering changing your company you should be aware that the pricing structures, services offered and policies will differ between the different companies.You should carefully check the information and contracts of the competing electricity suppliers, and compare these to your current terms, to make sure that you choose the best deal for your needs. A lot depends on your gas bills or electricity bill, and your location by postal code. You can also estimate bill impacts by applying tips from this guide on how to save electricity while comparing plans.

Dual fuel offers

Dual fuel is the supply of gas and electricity by the same company. Some gas and electricity suppliers are licensed separately by Ofgem to supply customers with both fuels. Some companies will supply both fuels under one contract, while others will give one contract for gas and another for electricity. For households with high usage, reviewing your typical electricity power consumption patterns can reveal whether dual fuel makes financial sense.

Electricity Suppliers who make dual offers will often give a discount off the total bill as they can make administrative savings by issuing combined bills and collecting combined payments. However, this does not necessarily mean that the cost of gas and electricity

procedures for complaints
payment of bills, arrangements for dealing with arrears and prepayment meters
site access procedures
energy efficiency advice
services for older, disabled and chronically sick people. As part of this code of practice, the company must keep a register of these people and provide services to help those who are blind and partially sighted or deaf or hearing impaired. Especially during a power outage, it is important that these customers are restored asap.The customer may have to pay for some of these services.
- how you will be charged for your electricity supply. Some companies may make a fixed standing charge and then a unit charge for the amount of electricity used; an company may not make a standing charge, but charge a higher unit price
- whether different charges apply to different periods during the day
- if cheaper prices are offered for particular payment methods, for example, if you pay by direct debit
- what service standards each company is offering, for example, for repairs, extra help for older or disabled customers.All electricity suppliers must keep a list of their customers who ask to be identified as pensioners, chronically sick or disabled.The electricity supplier must tell all its customers that it keeps such a list and give information on how customers can be added to the list
- the company's policies, for example, on debt and disconnection.

Electricity Today T&D Magazine Subscribe for FREE

Stay informed with the latest T&D policies and technologies.

Timely insights from industry experts
Practical solutions T&D engineers
Free access to every issue

Download the 2026 Electrical Training Catalog

Download the 2026 Electrical Training Catalog

Capacitance Explained