Voltage Drop Calculator

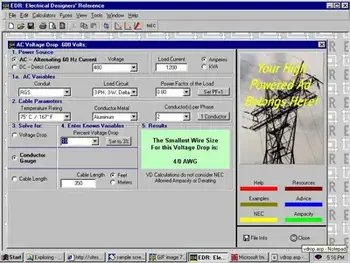
A voltage drop calculator helps electricians and engineers estimate line loss, wire size, and circuit efficiency. By inputting conductor length, current, and material, it ensures proper electrical design, safe voltage regulation, and compliance with power distribution standards.

What is a Voltage Drop Calculator?

A voltage drop calculator (VDC) is crucial for any electrical engineer or designer. It enables them to calculate VD accurately, which is essential for maintaining an efficient and safe electrical system.

✅ Quickly estimates voltage loss in electrical circuits

✅ Helps select the correct wire size for load and distance

✅ Supports NEC code compliance and system efficiency

Power Quality Analysis Training

Power Factor Training

Request a Free Power Quality Training Quotation

Voltage drop calculators are used in various applications, including residential, commercial, and industrial settings, and offer several benefits, such as accurate calculations, time savings, cost reduction, and hazard prevention. Additionally, engineers can ensure the electrical system operates efficiently and safely by considering factors such as cable sizing, wire gauge, and the type of conductor used. Want the full math? Visit our voltage drop formula guide for detailed equations and examples.

There are numerous VDCs available on the internet, and one of the best places to find them is on Google Play.

Applications of Voltage Drop Calculators

VDCs are used in various residential, commercial, and industrial applications. For instance, in residential applications, VDCs help determine the appropriate wire size for the electrical service panel, the length of wires, and the type of installation, ensuring that the electrical system operates correctly and safely. Additionally, VD formulas can be used to calculate resistance and reactance in both single-phase and three-phase electrical systems. It is measured in feet over a specified length.

In commercial applications, voltage drop calculators are used to design and maintain electrical systems in buildings such as hospitals, schools, and offices. These buildings require careful design to ensure that they meet the power requirements of the building and are safe for occupants. VDCs play a crucial role in this process by calculating the VD in the circuit and determining the appropriate wire size and other specifications.

In industrial applications, VDCs are used to design and maintain electrical systems in factories and other industrial settings. These systems require careful design to ensure they meet the equipment's power requirements and are safe for workers. VDCs determine the circuit's VD, the appropriate wire size, and other specifications to ensure that the electrical system operates efficiently and safely. For an overview of the general principles of voltage drop across AC and DC systems, read our article.

Benefits of Using a VDC

Using a VDC offers several benefits, including:

Accurate Calculations: VDCs use complex algorithms to calculate VD accurately. This ensures that the electrical system operates efficiently and safely.

Saves Time: VDCs save time by automating the process of calculating VD. This allows engineers to focus on other aspects of the design process, such as equipment selection and installation.

Reduces Costs: By accurately calculating VD, engineers can select the appropriate wire size and other specifications, thereby reducing the cost of the electrical system.

Prevents Hazards: Accurate calculation of VD prevents electrical hazards, including fires and shocks.

FREE Voltage Drop Calculator

Cable Sizing and Wire Gauge

One of the most critical factors to consider when designing an electrical system is cable sizing and wire gauge. The conductor's or wire gauge's size is critical in determining the amount of current that can flow through the conductor without causing excessive VD or overheating. American Wire Gauge (AWG) is the standard system used to specify wire sizes, providing a range of conductor sizes based on the wire's cross-sectional area. Additionally, the National Electrical Code (NEC) provides guidelines for ampacity and voltage drop (VD) for various conductor sizes and types of installations.

Copper or Aluminum Conductors

The type of conductor used in an electrical system also affects the voltage drop (VD). Copper and aluminum conductors are the most commonly used materials, with copper being preferred due to its lower resistance and higher conductivity. However, aluminum conductors are less expensive and commonly used in larger conductors and power transmission lines.

Frequently Asked Questions

How do I calculate voltage drop?

To calculate VD, you can use the VD formula, which is V = IR, where V is the voltage drop, I is the current flowing through the conductor, and R is the resistance of the conductor. By knowing the current, resistance, and length of the conductor, you can calculate the VD and determine whether it falls within acceptable limits.

How do I use it?

To use a VDC, you need to input the current flowing through the conductor, the length of the conductor, and the wire gauge or cable size. The tool then uses complex algorithms to calculate the VD in the circuit accurately. Based on the results, you can determine the appropriate wire size, cable length, and other specifications necessary to maintain an efficient and safe electrical system.

How is voltage drop calculated in a circuit?

VD is calculated in a circuit using Ohm's Law, which states that the VD across a conductor is equal to the product of the current and resistance. By knowing the current, resistance, and length of the conductor, you can calculate the VD and determine whether it falls within acceptable limits.

What factors affect voltage drop in a circuit?

The factors that affect VD in a circuit include the current flowing through the conductor, the length of the conductor, the resistance of the conductor, and the wire gauge or cable size. Other factors, such as the type of conductor and installation, can also affect VD.

EF Partner Media

Video

Three Methods to Measuring Winding Hot Spot Article

Who Invented Electricity? Catalog

Substation Product

Calisto R9 - High-accuracy and Low-maintenance Dissolved Gas Analysis (DGA) Monitor

Why is it important to calculate voltage drop?

Calculating VD is essential in maintaining an efficient and safe electrical system. VD can impact the performance of electrical equipment and devices, leading to hazards such as fires and electrical shock. By accurately calculating VD, engineers can select the appropriate wire size, cable length, and other necessary specifications to maintain an efficient and safe electrical system.

What are the benefits of using a VDC?

Using a VDC offers several benefits, including accurate calculations, time savings, cost reduction, and hazard prevention. By accurately calculating VD, engineers can select the appropriate wire size and other specifications, thereby reducing the cost of the electrical system. In addition, calculating VD accurately can prevent electrical hazards such as fires and shocks.

Are there any limitations to using a VDC?

While VDCs offer numerous benefits, they also have some limitations. For example, they rely on the accuracy of the input parameters, but may overlook other factors that can affect voltage drop, such as temperature and ambient conditions. Additionally, they may not be suitable for complex electrical systems.

What is the voltage drop per 100 ft?

The VD per 100 ft depends on various factors, including the current flowing through the conductor, the conductor's length, its resistance, and the wire gauge or cable size. Therefore, it is essential to calculate the VD accurately to determine the appropriate wire size and cable length necessary to maintain an efficient and safe electrical system.

What is a rule of thumb for voltage drop?

The rule of thumb for VD is that the VD in a circuit should not exceed 3% for power circuits and 5% for lighting circuits. These values are based on the National Electrical Code (NEC) guidelines, ensuring the electrical system operates efficiently and safely.

Southwire Voltage Drop Calculator

Related News

What is Medium Voltage iExplained

Medium voltage refers to electrical systems operating between 1 kV and 35 kV, used in industrial facilities, substations, and utility power distribution networks to safely transfer energy between low-voltage and high-voltage levels.

What is Medium Voltage?

Medium voltage refers to the electrical range between 1 kV and 35 kV, bridging the gap between low- and high-voltage systems for efficient energy transfer and safe power distribution across industrial, commercial, and utility applications.

✅ Used in substations, industrial plants, and utility grids

✅ Defined by IEEE and IEC classification standards

✅ Supports reliable energy transmission and electrical safety

A medium voltage (MV) system is crucial for distributing electricity in industrial, commercial, and institutional settings. It acts as the intermediary between high-voltage transmission lines and low-voltage consumer systems, ensuring efficient power delivery within a facility. This article provides a comprehensive overview of a medium voltage system, including its definition, applications, equipment, safety practices, and relevant standards. Understanding these concepts is vital for electrical professionals to ensure the safe and efficient operation of this critical power infrastructure. Medium voltage systems are essential links in 3 phase electricity networks, where balanced power delivery ensures efficient energy distribution across industrial and utility infrastructures.

Understanding medium voltage systems is essential for electrical professionals working in industrial, commercial, and institutional settings. This article provides a comprehensive overview of what constitutes medium voltage, its role in the power grid, common applications, and safety considerations. By grasping these key concepts, professionals can ensure the safe and efficient design, operation, and maintenance of these critical power systems. Understanding 3 phase power helps explain how medium voltage circuits maintain stable electrical loads in substations and manufacturing facilities.

Voltage Levels and Classifications

In the realm of electrical engineering, voltage levels are broadly categorized to distinguish their applications and safety requirements. These categories range from LV, typically used for residential applications, to extra high voltage (HV) and ultra-high voltages employed in HV transmission across long distances. MV occupies a middle ground, generally falling between 1,000 volts (600 volts in some instances) and 35,000 volts (35 kV). This distinguishes it from HV used in transmission and lower voltages used in end-user applications. Many 3 phase transformers and pad-mounted transformer installations operate at medium voltage levels, stepping electrical energy down for safe use in local distribution systems.

To better visualize this, imagine electricity flowing like a river through the electrical grid. V is like the force propelling the water, and different levels represent different sections of the river. HV is like a powerful, fast-flowing river capable of transporting electricity over long distances. MV, on the other hand, is like a branching stream that distributes the water (electricity) to various destinations. It's the crucial link between the high-powered transmission lines and the LV systems that deliver power to individual consumers. For a foundational understanding, review basic electricity concepts that explain how V, current, and resistance interact within medium voltage electrical systems.

What is Medium Voltage Applications?

Medium voltage systems have a wide range of applications in industrial, commercial, and institutional settings. In industrial facilities, they power large motors, heavy machinery, and industrial processes. Commercial buildings utilize what is MV for HVAC systems, lighting, and other electrical loads. Institutions such as hospitals and universities rely on MV to support their critical operations.

The use of MV is increasing. Historically, it was mainly used for subtransmission and primary distribution, supplying distribution transformers that step down the voltage to LV for end-use equipment. It was also traditionally used in industries for MV motors. However, with advancements in power electronics and semiconductor technology, new applications are emerging, such as:

MV DC Distribution Grids: These grids offer higher efficiency in long-distance transmission and are being implemented in collector grids for wind and photovoltaic parks.
Renewable Energy Integration: MV systems play a vital role in integrating renewable energy sources into the power grid, enabling the transition to a more sustainable energy future.

The principles of active power apply directly to medium voltage operations, where real power flow efficiency determines the overall performance of industrial and commercial grids.

Frequently Asked Questions

How does MV differ from low and HV?

Medium voltage occupies a middle ground between LV, typically used for residential applications, and HV, employed for long-distance transmission. It's the "in-between" voltage level that allows us to efficiently distribute power to different consumers.

What is Medium Voltage Range ?

Generally, MV falls between 1,000 volts (600 volts in some instances) and 35,000 volts (35 kV). This range can vary slightly depending on regional standards and practices. For example, ANSI standards in the US include voltages up to 69 kV in the MV class, while IEC standards use 1000 Vrms as the threshold between low and HV in AC installations.

What is MV in industrial, commercial, and institutional power systems?

Medium voltage is distributed within these facilities to power various equipment and loads. It's the primary level used within these settings before being stepped down to LV for end-use.

What are common applications of MV systems?

Common applications include powering large motors and machinery in industrial settings, as well as HVAC and lighting systems in commercial buildings, and critical operations in institutions such as hospitals. Emerging applications include microgrids and the integration of renewable energy.

What are the key standards and regulations governing MV systems?

Key standards include those from ANSI, IEEE, and NEC, which provide guidelines for the design, installation, and safety of MV systems. These standards ensure that MV systems are implemented in a safe and consistent manner.

A Medium Voltage system is crucial for distributing electricity in industrial, commercial, and institutional settings. It acts as the intermediary between HV transmission lines and LV consumer systems, ensuring efficient power delivery within a facility. This article provides a comprehensive overview of a medium voltage system, including its definition, applications, equipment, safety practices, and relevant standards. Understanding these concepts is vital for electrical professionals to ensure the safe and efficient operation of this critical power infrastructure.

Electrical Energy

Electrical energy is the power derived from the movement of electrons through a conductor. It powers homes, industries, and modern technology. This form of energy can be generated from various sources, including fossil fuels, solar, wind, and hydroelectric systems.

What is Electrical Energy?

Electrical energy is the result of electric charge flow, used to perform work in countless applications across daily life and industry.

✅ Powers lighting, heating, and electronic devices across all sectors

✅ Generated by power plants from renewable and non-renewable sources

✅ Converted from and into other energy forms, like mechanical or thermal

Electrical Energy: The Fundamental Source of Power

An Electric charge is a property of certain subatomic particles (e.g., electrons and protons) which interacts with the electromagnetic field and causes attractive and repulsive forces between them. Electric charges give rise to one of the four fundamental forces of nature, and is a conserved property of matter that can be quantified. In this sense, the phrase "quantity of electricity" is used interchangeably with the phrases "charge of electricity" and "quantity of charge." There are two types of charge: we call one kind of charge positive and the other negative. Through experimentation, we find that like-charged objects repel and opposite-charged objects attract one another. Coulomb's law gives the magnitude of the force of attraction or repulsion. For a broader understanding, visit how electricity works to see how it is generated, transmitted, and used across power grids and homes.

How Electric Fields Transfer Energy Between Charges

Michael Faraday introduced the concept of the Electrical Energy field. The field force acts between two charges, in the same way that the gravitational field force acts between two masses. However, the electric field is a little bit different. Gravitational force depends on the masses of two bodies, whereas the electromagnetic force depends on the electric charges of two bodies. While gravity can only pull two masses together, the force can be attractive or repulsive. If both charges are of the same sign (e.g. both positive), there will be a repulsive force between the two. If the charges are opposite, an attractive force will exist between the two bodies (as seen in static electricity and kinetic energy). The magnitude of the force varies inversely with the square of the distance between the two bodies and is also proportional to the product of the unsigned magnitudes of the two charges. Discover how electrical load determines the demand placed on a system’s energy supply.

Electrical Energy and Voltage Explained

The electric potential difference between two points is defined as the work done per unit charge (against forces) in moving a positive point charge slowly from one point to another. Choose one point as a reference with zero potential. The electric potential at any other point equals the work required per unit charge to move a positive test charge from the reference point to that location. For isolated charges, the reference point is usually taken to be infinity. The potential is measured in volts. (1 volt = 1 joule/coulomb) The electric potential is analogous to temperature: there is a different potential at every point in space, and the potential gradient indicates the direction and magnitude of the driving force behind electric current flow. Similarly, there is an electric potential at every point in space, and its gradient indicates the direction and magnitude of the driving force behind the movement of charged energy. To understand how voltage influences electrical energy, it's essential to grasp how potential difference drives current through circuits.

Electric Current: Flow of Charge That Powers Technology

Current is a flow of electrical energy, and its intensity is measured in amperes. Examples of electric currents include metallic conduction, where electrons flow through a conductor such as a metal wire, and electrolysis, where ions (charged atoms) flow through liquids. The particles themselves often have energy to move quite slowly, while the moving electric field that drives them propagates at close to the speed of light. See energy conduction for more information. Alternating current and direct current each transfer electrical energy differently, depending on the application.

Devices that utilize charge flow principles in materials are referred to as electronic devices.

A direct current (DC) is a unidirectional flow, while an alternating current (AC) reverses direction repeatedly. The time average of an alternating current is zero, but its capability (RMS value) is not zero.

Ohm's Law is an important relationship describing the behaviour of energy, relating it to voltage. Explore the principles behind Ohm’s Law to see how voltage, current, and resistance interrelate in determining energy flow. Learn how electrical resistance affects energy loss and heat generation in systems.

For historical reasons, power is said to flow from the most positive part of a circuit to the most negative part. The current thus defined is referred to as conventional current. It is now known that, depending on the conditions, a current can consist of a flow of charged particles in either direction, or even in both directions at once. The positive-to-negative convention is widely used to simplify this situation. If another definition is used - for example, "electron current" - it should be explicitly stated.

Watt’s Law - Power Triangle

Watt’s Law defines the relationship between power (watts), voltage (volts), and current (amps): Power = Voltage × Current. It’s used in electrical calculations to determine energy usage, system efficiency, and safe equipment ratings in both residential and industrial systems.

What is: Watt’s Law?

Watt’s Law is a fundamental principle in electrical engineering:

✅ Calculates electrical power as the product of voltage and current

✅ Helps design efficient and safe electrical systems

✅ Used in both residential and industrial applications

Watt’s Law is a fundamental principle in electrical engineering that defines the relationship between power, voltage, and current in an electrical circuit. James Watt invented the law. It states that the power (measured in watts) of an electrical device is equal to the product of the voltage (measured in volts) and the current (measured in amperes) flowing through it. In other words, the watt's law formula is expressed as: Power = Voltage × Current. This simple equation is essential for understanding how electrical components consume and distribute energy in a circuit.

For example, consider a light bulb connected to an electrical circuit. The electrical potential (voltage) pushes the electric charge through the filament of the bulb, creating a flow of electrons (current). As the electrons flow, they generate heat and light, representing the bulb’s power in a circuit. By knowing the voltage and current, you can easily calculate the power output of the bulb. The wattage of the bulb indicates the energy consumed per second.

Practical applications of this formula are vast. This equation is especially useful in designing safe and efficient electrical systems. For instance, designing the wiring for both small devices and large power systems requires a thorough understanding of the relationship between voltage, current, and power. The formula helps ensure that systems are capable of delivering the required energy without causing failures or inefficiencies.

Ohm’s Law and this principle are often used together in electrical engineering. While power focuses on the relationship between voltage and current, Ohm’s Law deals with the relationship between voltage, current, and resistance (measured in ohms). Ohm’s Law states that voltage equals current multiplied by resistance (Voltage = Current × Resistance). By combining Ohm’s Law and this power equation, you can analyze an electrical system more comprehensively. For example, if you know the voltage and resistance in a circuit, you can calculate the current and then determine the power in the circuit. To fully understand Watt's Law, it helps to explore how voltage and current electricity interact in a typical electrical circuit.

Georg Simon Ohm – German physicist and mathematician (1787–1854), known for Ohm's Law, relating voltage, current, and resistance.

What is Watt's Law and how is it used in electrical circuits?

Watt’s Law is a fundamental principle in electrical engineering that defines the relationship between power, voltage, and current in an electrical circuit. The formula is expressed as:

Power (Watts) = Voltage (Volts) × Current (Amperes)

In simpler terms, Watt’s Law states that the electrical power consumed by a device (measured in watts) is the product of the electrical potential difference (voltage) and the current flowing through the circuit. Accurate calculations using Watt’s Law often require a voltage-drop calculator to account for line losses in long-distance wiring. Comparing voltage drop and voltage sag conditions illustrates how slight changes in voltage can have a substantial impact on power output.

James Watt – Scottish inventor and mechanical engineer (1736–1819), whose improvements to the steam engine led to the naming of the watt (unit of power).

How is it used? Watt’s Law is widely used to determine the amount of power an electrical device or system consumes. This is especially important for designing electrical circuits, optimizing power distribution, and ensuring the efficiency of devices. Here are a few examples of how it’s applied:

Electrical Circuit Design: Engineers use it to calculate the power consumption of devices and ensure that circuits can handle the expected electrical load. This helps prevent overloads and ensures that the wiring is safe.
Power Output Calculations: Using this formula, you can calculate the power output of a generator, appliance, or device, enabling you to match the right components to your system's requirements.
Energy Efficiency: Understanding power consumption in appliances and devices helps consumers make informed choices, such as selecting energy-efficient options. Devices like wattmeters and watthour meters measure power and energy usage based directly on the principles of Watt’s Law. For a deeper look at how devices like ammeters help measure current, see how their readings plug directly into Watt’s Law calculations.

How is Watt's Law different from Ohm's Law?

Watt’s Law and Ohm’s Law are both fundamental principles in electrical engineering, but they deal with different aspects of electrical systems:

Watt’s Law defines the relationship between power, voltage, and current. It focuses on the amount of energy used by a device in a given circuit. The formula is:

Power = Voltage × Current

Ohm’s Law defines the relationship between voltage, current, and resistance in a circuit. Ohm’s Law explains how the current is affected by the voltage and the resistance present in the circuit. The formula for Ohm’s Law is:

Voltage = Current × Resistance

Key Differences:

Focus: It focuses on power, while Ohm’s Law focuses on the flow of electricity in a circuit, particularly how resistance affects current.
Watt’s Law is used to determine the amount of power a device is consuming. Ohm’s Law, on the other hand, is used to calculate current, voltage, or resistance in a circuit depending on the other known variables.
Applications: It is applied when designing systems that require power management, such as calculating the power output or efficiency of devices. Ohm’s Law is used more in analyzing how current behaves in a circuit when different resistive elements are present.

By combining both laws, electrical engineers can gain a comprehensive understanding of how electrical systems function, ensuring that devices operate efficiently and safely. When used with Ohm’s Law, Watt's Law enables engineers to analyze both energy consumption and electrical resistance.

One key area of application is in energy consumption. By understanding the voltage and current values for a specific device, engineers can monitor the amount of energy the device consumes. This is especially important for managing energy usage in homes, businesses, and power systems. By applying the formula, you can identify inefficient devices and make more informed decisions about energy efficiency.

In renewable energy systems, such as solar panels and wind turbines, this principle plays a critical role in optimizing energy output. Engineers use the formula to calculate how much electrical energy is being generated and distributed. This is crucial for ensuring that power systems operate efficiently and minimize excess energy loss.

Another practical application of this formula is in the automotive industry. It is used to design vehicle charging systems and battery technologies. For example, electric vehicle (EV) charging stations depend on understanding voltage, current, and power to ensure efficient charging times. Engineers use the equation to calculate the charging capacity required for EV batteries, helping to create optimal charging solutions.

In large facilities like data centers, this Watt’s Law formula is used to ensure power distribution is efficient. By applying the relationship between power, voltage, and current, engineers can effectively manage power systems, thereby reducing energy consumption and operational costs. Proper energy management in data centers is crucial, as high power usage can result in significant energy costs.

This power formula is indispensable for electrical engineers and technicians. The applications of Watt’s Law extend across various industries and are utilized in everything from designing power system wiring to developing renewable energy technologies. By combining Ohm’s Law and this principle, electrical engineers can optimize the performance of electrical components, ensuring energy efficiency and system reliability. Understanding the role of a resistor in a circuit can reveal how power is dissipated as heat, a key concept derived from Watt’s Law.

Finally, visual tools like the Watt's Law triangle are often used to simplify the application of this principle, helping both professionals and students understand how to apply the formula. As technology advances and energy demands grow, this formula remains a key element in electrical engineering, guiding the development of more efficient systems for the future.

Resistance Formula Explained

The resistance formula, R = V/I, shows how voltage and current determine opposition in a circuit. Central to Ohm’s Law, it is widely applied in electronics, power distribution, and engineering to calculate resistance, ensure efficiency, and design reliable electrical systems.

What is a Resistance Formula?

The resistance formula is a vital tool in understanding and optimizing electrical circuits. By analyzing the interplay between Ohm's law, conductor material, wire length, cross-sectional area, and temperature, we can manipulate Resistance to improve circuit performance. Balancing these factors ensures the efficient flow of electrons, minimizes energy loss, and maximizes the effectiveness of our electrical devices.

✅ R = V/I links voltage, current, and resistance

✅ Essential for circuit analysis and design

✅ Applied in electronics, power systems, and physics

Electrical circuits are essential for powering our daily lives, and understanding the factors that influence their performance is key to optimizing their efficiency. A critical aspect of electrical circuits is the Resistance they encounter, which directly affects the flow of electrons. Based on Ohm's law, the formula helps us analyze and manipulate various elements within a circuit. Topics like electrical resistance and the unit of electrical resistance expand on how opposition to current flow is measured and applied in engineering.

The flow of charge in any conductor depends on material properties and circuit design, where individual resistances combine differently depending on series or parallel circuit arrangements. According to law resistance principles, the total parallel resistance is always less than the smallest branch, and values are measured as resistance in ohms. Materials with the smallest resistivities like copper conduct efficiently, though their performance is affected by the temperature coefficient of resistivity, which alters conduction as heat rises. For visual examples and diagrams, resources such as Wikimedia Commons provide helpful illustrations.

Ohm's Law

Ohm's law is fundamental to understanding electrical circuits. It states that the Voltage across a conductor is directly proportional to the electric Current passing through it, and the constant of proportionality is the electrical Resistance. In mathematical terms, Ohm's law can be expressed as V = IR, where V is the Voltage, I is the electric Current, and R is the Resistance. Related principles, including Ampere’s Law and the Biot-Savart Law, further explain how current and magnetic fields interact with resistance in circuits.

The formula R = ρ(L/A) is derived from Ohm's law and describes how R depends on the conductor's material, length (L), and cross-sectional area (A). The resistivity (ρ) is a property unique to the conductor material and represents its ability to impede the flow of electrons. Different materials, such as copper or aluminum, have different resistivities, affecting the overall electrical R.

Wire length and cross-sectional area play a significant role in determining a conductor's R. As the wire length increases, so does the R, as electrons face more obstacles. Conversely, increasing the cross-sectional area reduces R, allowing more electrons to flow through the conductor simultaneously. This inverse relationship between R and cross-sectional area is vital in designing circuits to minimize energy loss and optimize efficiency.

Various factors influence the resistivity of conductor material. For instance, impurities in the material can hinder electron flow, thereby increasing resistivity. Additionally, the arrangement of atoms within the material's lattice structure affects the ease with which electrons can pass. Finally, the temperature coefficient is crucial, as fluctuations can alter resistivity. Generally, R increases with higher temperatures as atoms vibrate more and impede electron flow.

Resistance and conductance differ in their relationship to the flow of electrons. While R quantifies the opposition a conductor presents to the flow of electrons, conductance represents the ease with which electrons can pass. Mathematically, conductance (G) is the reciprocal of Resistance (R), and is measured in Siemens (S):

G = 1/R

The formula can be used to calculate power dissipation in a circuit. Power (P) is the product of Voltage (V) and current (I): P = VI. Using Ohm's law, we can substitute V = IR into the power formula to obtain P = I^2R. This equation demonstrates that higher R results in greater power dissipation, manifesting as heat. Hence, managing R is essential in preventing energy loss and maintaining circuit efficiency.

Ohm's law defines a mathematical relationship involving V, R, and current (I) within an electrical component. Ohm, denoted by the Greek letter omega (Ω), is the unit of measurement for R. Furthermore, Ohm's law can derive a power equation by computing electrical power, quantified in watts. Subsequently, Gustav Kirchhoff built upon Ohm's foundational work and introduced Kirchhoff's rules, two equalities addressing current and Voltage in an electric circuit model.

Ohm's law outlines the fundamental principles of electrical circuits, highlighting the interdependence between voltage, current, and resistance. This relationship can be expressed in three different formulas:

V = I × R (Voltage equals Current multiplied by Resistance)
R = V / I (Resistance equals Voltage divided by Current)
I = V / R (Current equals Voltage divided by Resistance)

These formulas illustrate the interconnection of voltage, current, and resistance in electrical circuits. By manipulating these relationships, we can analyze the behaviour of circuits, troubleshoot issues, and optimize efficiency.

The significance of Ohm's law extends beyond its mathematical representation. It forms the basis for understanding various electrical phenomena, including power dissipation, energy consumption, and the impact of R on the performance of electrical components. The role of resistance is closely tied to capacitance and inductance, which determine energy storage and reactance in alternating current systems.

As we explore the vast applications of electrical circuits, understanding the formula allows us to make informed decisions in choosing conductor materials, adjusting wire length and cross-sectional area, and considering temperature fluctuations. With an understanding of how these factors interact, we can continue to innovate, create, and harness the power of electricity to achieve a brighter future.

Voltage Drop Calculator